ಸಂಪೂರ್ಣ ಸರಪಳಿಗಾಗಿ ಮತ್ತು ಸರಪಳಿಯ ಒಂದು ವಿಭಾಗಕ್ಕೆ ಓಮ್ನ ನಿಯಮ: ಸೂತ್ರ ಆಯ್ಕೆಗಳು, ವಿವರಣೆ ಮತ್ತು ವಿವರಣೆ

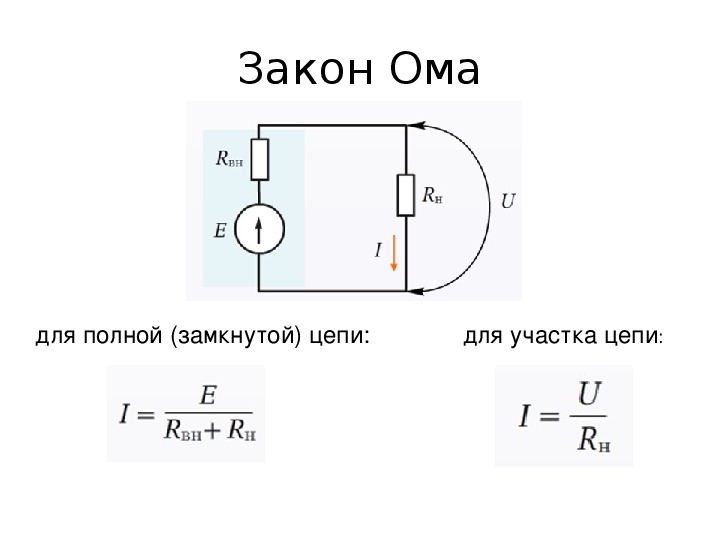
ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ಗಾಗಿ

ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ ಎಂದರೆ ಮುಚ್ಚಿದ ವಿದ್ಯುತ್ ಸಂಪರ್ಕ, ಅದರ ಮೂಲಕ ಪ್ರಸ್ತುತ ಪರಿಚಲನೆಯಾಗುತ್ತದೆ. ತಂತಿಗಳ ಸರಣಿಯು ಪರಸ್ಪರ ಸಂಪರ್ಕಿಸಿದಾಗ ಮತ್ತು ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಪೂರ್ಣಗೊಳಿಸಿದಾಗ ನಾನು ವೃತ್ತದ ಒಂದು ತುದಿಯಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಓಡುತ್ತೇನೆ, ಅದು ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ ಆಗಿರುತ್ತದೆ.

EMF (E) - ವೋಲ್ಟ್‌ಗಳಲ್ಲಿ ಸೂಚಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಅಳೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಫ್ಯಾರಡೆ ನಿಯಮದ ಪ್ರಕಾರ ಬ್ಯಾಟರಿ ಅಥವಾ ಕಾಂತೀಯ ಬಲದಿಂದ ಉತ್ಪತ್ತಿಯಾಗುವ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಉಲ್ಲೇಖಿಸುತ್ತದೆ, ಇದು ಸಮಯ-ಬದಲಾಗುವ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ಪ್ರೇರೇಪಿಸುತ್ತದೆ ಎಂದು ಹೇಳುತ್ತದೆ.

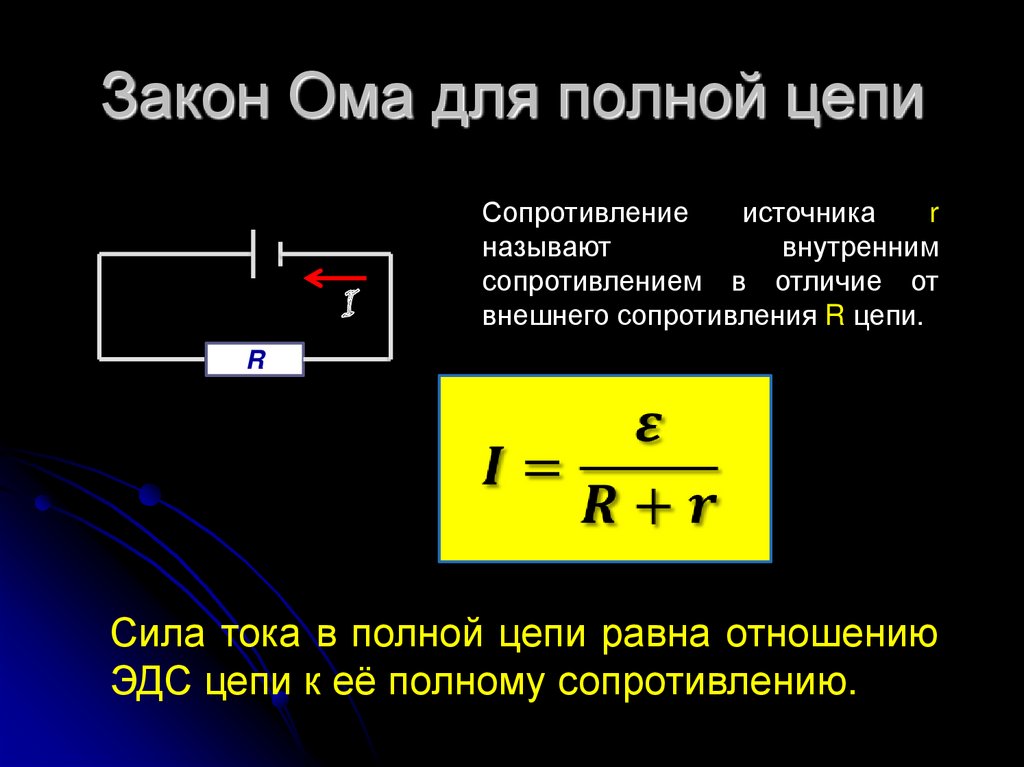
ನಂತರ: E = IR + Ir

E \u003d I (R + r)

I \u003d E / (R + r)

ಎಲ್ಲಿ: r ಎಂಬುದು ಪ್ರಸ್ತುತ ಮೂಲದ ಪ್ರತಿರೋಧವಾಗಿದೆ.

ಈ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಮುಚ್ಚಿದ ಲೂಪ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳ ಓಮ್‌ನ ನಿಯಮ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ವೈವಿಧ್ಯಮಯ ಸರಪಳಿ

ಪ್ರತ್ಯೇಕ ವಿಭಾಗ ಮತ್ತು ಸಂಪೂರ್ಣ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್

ಒಂದು ವಿಭಾಗ ಅಥವಾ ಸಂಪೂರ್ಣ ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಅನ್ವಯಿಸಿದಂತೆ ಓಮ್‌ನ ನಿಯಮವನ್ನು ಎರಡು ಲೆಕ್ಕಾಚಾರದ ಆಯ್ಕೆಗಳಲ್ಲಿ ಪರಿಗಣಿಸಬಹುದು:

• ಪ್ರತ್ಯೇಕ ಸಣ್ಣ ವಿಭಾಗ. ಇದು EMF ಮೂಲವಿಲ್ಲದ ಸರ್ಕ್ಯೂಟ್‌ನ ಭಾಗವಾಗಿದೆ.
• ಒಂದು ಅಥವಾ ಹೆಚ್ಚಿನ ವಿಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಸಂಪೂರ್ಣ ಸರಪಳಿ. ಇದು ತನ್ನದೇ ಆದ ಆಂತರಿಕ ಪ್ರತಿರೋಧದೊಂದಿಗೆ EMF ಮೂಲವನ್ನು ಸಹ ಒಳಗೊಂಡಿದೆ.

ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಪ್ರಸ್ತುತ ವಿಭಾಗದ ಲೆಕ್ಕಾಚಾರ

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಮೂಲ ಸೂತ್ರ I \u003d U / R ಅನ್ನು ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ, ಇದರಲ್ಲಿ I ಪ್ರಸ್ತುತ ಶಕ್ತಿ, U ವೋಲ್ಟೇಜ್, R ಎಂಬುದು ಪ್ರತಿರೋಧ. ಅದರ ಪ್ರಕಾರ, ಓಮ್ನ ನಿಯಮದ ಸಾಮಾನ್ಯವಾಗಿ ಅಂಗೀಕರಿಸಲ್ಪಟ್ಟ ವ್ಯಾಖ್ಯಾನವನ್ನು ಒಬ್ಬರು ರೂಪಿಸಬಹುದು:

ಈ ಸೂತ್ರೀಕರಣವು ಗ್ರಾಫಿಕ್ ವಿನ್ಯಾಸದಲ್ಲಿ "ಕ್ಯಾಮೊಮೈಲ್" ಎಂದು ಕರೆಯಲ್ಪಡುವ ಅನೇಕ ಇತರ ಸೂತ್ರಗಳಿಗೆ ಆಧಾರವಾಗಿದೆ. ಸೆಕ್ಟರ್ ಪಿ - ಪವರ್ ಅನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ, ಕ್ಷೇತ್ರಗಳಲ್ಲಿ I, U ಮತ್ತು R - ಪ್ರಸ್ತುತ ಶಕ್ತಿ, ವೋಲ್ಟೇಜ್ ಮತ್ತು ಪ್ರತಿರೋಧಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಕ್ರಮಗಳನ್ನು ಕೈಗೊಳ್ಳಲಾಗುತ್ತದೆ.

ಪ್ರತಿಯೊಂದು ಅಭಿವ್ಯಕ್ತಿ - ಮೂಲಭೂತ ಮತ್ತು ಹೆಚ್ಚುವರಿ ಎರಡೂ, ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಬಳಸಲು ಉದ್ದೇಶಿಸಿರುವ ಅಂಶಗಳ ನಿಖರವಾದ ನಿಯತಾಂಕಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನಿಮಗೆ ಅನುಮತಿಸುತ್ತದೆ.

ಎಲೆಕ್ಟ್ರಿಕಲ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುವ ತಜ್ಞರು ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವ ತ್ರಿಕೋನ ವಿಧಾನವನ್ನು ಬಳಸಿಕೊಂಡು ಯಾವುದೇ ನಿಯತಾಂಕಗಳ ತ್ವರಿತ ನಿರ್ಣಯವನ್ನು ನಿರ್ವಹಿಸುತ್ತಾರೆ.

ಲೆಕ್ಕಾಚಾರಗಳು ವಿಭಾಗದ ಅಂಶಗಳನ್ನು ಸಂಪರ್ಕಿಸುವ ವಾಹಕಗಳ ಪ್ರತಿರೋಧವನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಅವುಗಳನ್ನು ವಿಭಿನ್ನ ವಸ್ತುಗಳಿಂದ ಮಾಡಲಾಗಿರುವುದರಿಂದ, ಈ ನಿಯತಾಂಕವು ಪ್ರತಿ ಸಂದರ್ಭದಲ್ಲಿಯೂ ವಿಭಿನ್ನವಾಗಿರುತ್ತದೆ.ಸಂಪೂರ್ಣ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ರೂಪಿಸಲು ಅಗತ್ಯವಿದ್ದರೆ, ಮುಖ್ಯ ಸೂತ್ರವು ವೋಲ್ಟೇಜ್ ಮೂಲದ ನಿಯತಾಂಕಗಳೊಂದಿಗೆ ಪೂರಕವಾಗಿದೆ, ಉದಾಹರಣೆಗೆ, ಬ್ಯಾಟರಿ.

ಸಂಪೂರ್ಣ ಸರಪಳಿಗಾಗಿ ಲೆಕ್ಕಾಚಾರದ ಆಯ್ಕೆ

ಸಂಪೂರ್ಣ ಸರ್ಕ್ಯೂಟ್ ಪ್ರತ್ಯೇಕ ವಿಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ, ವೋಲ್ಟೇಜ್ ಮೂಲ (EMF) ನೊಂದಿಗೆ ಒಂದೇ ಒಟ್ಟಾರೆಯಾಗಿ ಸಂಯೋಜಿಸಲಾಗಿದೆ. ಹೀಗಾಗಿ, ವಿಭಾಗಗಳ ಅಸ್ತಿತ್ವದಲ್ಲಿರುವ ಪ್ರತಿರೋಧವು ಸಂಪರ್ಕಿತ ಮೂಲದ ಆಂತರಿಕ ಪ್ರತಿರೋಧದಿಂದ ಪೂರಕವಾಗಿದೆ. ಆದ್ದರಿಂದ, ಮೊದಲು ಚರ್ಚಿಸಿದ ಮುಖ್ಯ ವ್ಯಾಖ್ಯಾನವು ಈ ಕೆಳಗಿನಂತೆ ಓದುತ್ತದೆ: I = U / (R + r). ಇಲ್ಲಿ, EMF ಮೂಲದ ಪ್ರತಿರೋಧಕ ಸೂಚಕ (r) ಅನ್ನು ಈಗಾಗಲೇ ಸೇರಿಸಲಾಗಿದೆ.

ಶುದ್ಧ ಭೌತಶಾಸ್ತ್ರದ ದೃಷ್ಟಿಕೋನದಿಂದ, ಈ ಸೂಚಕವನ್ನು ಬಹಳ ಕಡಿಮೆ ಮೌಲ್ಯವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಸಂಕೀರ್ಣ ಸರ್ಕ್ಯೂಟ್‌ಗಳು ಮತ್ತು ಸರ್ಕ್ಯೂಟ್‌ಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ, ಹೆಚ್ಚುವರಿ ಪ್ರತಿರೋಧವು ಕೆಲಸದ ನಿಖರತೆಯ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುವುದರಿಂದ ತಜ್ಞರು ಅದನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವಂತೆ ಒತ್ತಾಯಿಸಲಾಗುತ್ತದೆ. ಇದರ ಜೊತೆಗೆ, ಪ್ರತಿ ಮೂಲದ ರಚನೆಯು ತುಂಬಾ ವೈವಿಧ್ಯಮಯವಾಗಿದೆ, ಇದರ ಪರಿಣಾಮವಾಗಿ, ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ ಪ್ರತಿರೋಧವನ್ನು ಸಾಕಷ್ಟು ಹೆಚ್ಚಿನ ದರಗಳಿಂದ ವ್ಯಕ್ತಪಡಿಸಬಹುದು.

ಮೇಲಿನ ಲೆಕ್ಕಾಚಾರಗಳನ್ನು DC ಸರ್ಕ್ಯೂಟ್ಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ನಡೆಸಲಾಗುತ್ತದೆ. ಪರ್ಯಾಯ ಪ್ರವಾಹದೊಂದಿಗೆ ಕ್ರಿಯೆಗಳು ಮತ್ತು ಲೆಕ್ಕಾಚಾರಗಳನ್ನು ವಿಭಿನ್ನ ಯೋಜನೆಯ ಪ್ರಕಾರ ಮಾಡಲಾಗುತ್ತದೆ.

ವೇರಿಯಬಲ್ ಮೇಲೆ ಕಾನೂನಿನ ಪರಿಣಾಮ

ಪರ್ಯಾಯ ಪ್ರವಾಹದೊಂದಿಗೆ, ಸರ್ಕ್ಯೂಟ್ನ ಪ್ರತಿರೋಧವು ಪ್ರತಿರೋಧ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ, ಇದು ಸಕ್ರಿಯ ಪ್ರತಿರೋಧ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಪ್ರತಿರೋಧಕ ಲೋಡ್ ಅನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ಇದು ಅನುಗಮನದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುವ ಅಂಶಗಳ ಉಪಸ್ಥಿತಿ ಮತ್ತು ಸೈನುಸೈಡಲ್ ಪ್ರಸ್ತುತ ಮೌಲ್ಯದಿಂದಾಗಿ. ವೋಲ್ಟೇಜ್ ಸಹ ವೇರಿಯಬಲ್ ಆಗಿದೆ, ಅದರ ಸ್ವಿಚಿಂಗ್ ನಿಯಮಗಳ ಪ್ರಕಾರ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.

ಆದ್ದರಿಂದ, ಓಮ್ನ ಕಾನೂನಿನ ಪ್ರಕಾರ ಎಸಿ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟ ಪರಿಣಾಮಗಳನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ: ವೋಲ್ಟೇಜ್ನಿಂದ ಪ್ರಸ್ತುತದ ಪ್ರಮಾಣವನ್ನು ಮುನ್ನಡೆಸುವುದು ಅಥವಾ ವಿಳಂಬಗೊಳಿಸುವುದು, ಹಾಗೆಯೇ ಸಕ್ರಿಯ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಶಕ್ತಿಯ ಉಪಸ್ಥಿತಿ.ಪ್ರತಿಯಾಗಿ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕತೆಯು ಇಂಡಕ್ಟಿವ್ ಅಥವಾ ಕೆಪ್ಯಾಸಿಟಿವ್ ಘಟಕಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ.

ಈ ಎಲ್ಲಾ ವಿದ್ಯಮಾನಗಳು Z \u003d U / I ಅಥವಾ Z \u003d R + J * (XL - XC) ಸೂತ್ರಕ್ಕೆ ಅನುಗುಣವಾಗಿರುತ್ತವೆ, ಇದರಲ್ಲಿ Z ಪ್ರತಿರೋಧಕವಾಗಿದೆ; ಆರ್ - ಸಕ್ರಿಯ ಲೋಡ್; XL, XC - ಇಂಡಕ್ಟಿವ್ ಮತ್ತು ಕೆಪ್ಯಾಸಿಟಿವ್ ಲೋಡ್ಗಳು; ಜೆ ತಿದ್ದುಪಡಿ ಅಂಶವಾಗಿದೆ.

ಸಂಪೂರ್ಣ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಇಎಮ್‌ಎಫ್ ಮೂಲ

ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಸಂಭವಕ್ಕಾಗಿ, ಈ ಸರ್ಕ್ಯೂಟ್ ಕನಿಷ್ಠ ಒಂದು ವಿಶೇಷ ಅಂಶವನ್ನು ಹೊಂದಿರಬೇಕು, ಅದರಲ್ಲಿ ಅದರ ಧ್ರುವಗಳ ನಡುವೆ ಶುಲ್ಕವನ್ನು ವರ್ಗಾವಣೆ ಮಾಡುವ ಕೆಲಸ ನಡೆಯುತ್ತದೆ. ಈ ಅಂಶದ ಒಳಗೆ ಚಾರ್ಜ್‌ಗಳನ್ನು ಸಾಗಿಸುವ ಶಕ್ತಿಗಳು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ವಿರುದ್ಧ ಹಾಗೆ ಮಾಡುತ್ತವೆ, ಅಂದರೆ ಅವುಗಳ ಸ್ವಭಾವವು ವಿದ್ಯುತ್‌ಗಿಂತ ಭಿನ್ನವಾಗಿರಬೇಕು. ಆದ್ದರಿಂದ, ಅಂತಹ ಶಕ್ತಿಗಳನ್ನು ಮೂರನೇ ವ್ಯಕ್ತಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಅಕ್ಕಿ. 1. ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ ಬಾಹ್ಯ ಶಕ್ತಿಗಳು.

ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಕ್ರಿಯೆಯ ವಿರುದ್ಧ ಆರೋಪಗಳನ್ನು ವರ್ಗಾಯಿಸಲು ಬಾಹ್ಯ ಶಕ್ತಿಗಳು ಕಾರ್ಯನಿರ್ವಹಿಸುವ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಅಂಶವನ್ನು ಪ್ರಸ್ತುತ ಮೂಲ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಇದರ ಮುಖ್ಯ ಲಕ್ಷಣವೆಂದರೆ ಬಾಹ್ಯ ಶಕ್ತಿಗಳ ಪ್ರಮಾಣ. ಇದನ್ನು ನಿರೂಪಿಸಲು, ವಿಶೇಷ ಅಳತೆಯನ್ನು ಪರಿಚಯಿಸಲಾಗಿದೆ - ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ (EMF), ಇದನ್ನು $\mathscr{E}$ ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ಪ್ರಸ್ತುತ ಮೂಲದ ಇಎಮ್‌ಎಫ್‌ನ ಮೌಲ್ಯವು ಈ ಚಾರ್ಜ್‌ನ ಮೌಲ್ಯಕ್ಕೆ ಚಾರ್ಜ್‌ನ ವರ್ಗಾವಣೆಗೆ ಬಾಹ್ಯ ಶಕ್ತಿಗಳ ಅನುಪಾತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

$$\mathscr{E}={A_{st}\ಮೇಲೆ q}$$

ಇಎಮ್‌ಎಫ್‌ನ ಅರ್ಥವು ವಿದ್ಯುತ್ ವೋಲ್ಟೇಜ್‌ನ ಅರ್ಥಕ್ಕೆ ತುಂಬಾ ಹತ್ತಿರವಾಗಿರುವುದರಿಂದ (ಮರುಪಡೆಯಿರಿ, ವೋಲ್ಟೇಜ್ ಈ ಚಾರ್ಜ್‌ನ ಮೌಲ್ಯಕ್ಕೆ ಚಾರ್ಜ್ ಅನ್ನು ಸಾಗಿಸುವ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದಿಂದ ಮಾಡಿದ ಕೆಲಸದ ಅನುಪಾತವಾಗಿದೆ), ನಂತರ ವೋಲ್ಟೇಜ್‌ನಂತೆ ಇಎಮ್‌ಎಫ್ ಅನ್ನು ಅಳೆಯಲಾಗುತ್ತದೆ ವೋಲ್ಟ್‌ಗಳು:

$$1B={J\overCl}$$

ನೈಜ ಪ್ರಸ್ತುತ ಮೂಲದ ಎರಡನೆಯ ಪ್ರಮುಖ ವಿದ್ಯುತ್ ಗುಣಲಕ್ಷಣವೆಂದರೆ ಅದರ ಆಂತರಿಕ ಪ್ರತಿರೋಧ.ಟರ್ಮಿನಲ್ಗಳ ನಡುವೆ ಶುಲ್ಕಗಳನ್ನು ವರ್ಗಾಯಿಸಿದಾಗ, ಅವರು ಇಎಮ್ಎಫ್ ಮೂಲದ ವಸ್ತುವಿನೊಂದಿಗೆ ಸಂವಹನ ನಡೆಸುತ್ತಾರೆ ಮತ್ತು ಆದ್ದರಿಂದ, ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಮೂಲವು ಕೆಲವು ಪ್ರತಿರೋಧವನ್ನು ಒದಗಿಸುತ್ತದೆ. ಸಾಮಾನ್ಯ ಪ್ರತಿರೋಧದಂತೆ ಆಂತರಿಕ ಪ್ರತಿರೋಧವನ್ನು ಓಮ್‌ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ, ಆದರೆ ಇದನ್ನು ಸಣ್ಣ ಲ್ಯಾಟಿನ್ ಅಕ್ಷರ $r$ ನಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ಅಕ್ಕಿ. 2. ಪ್ರಸ್ತುತ ಮೂಲಗಳ ಉದಾಹರಣೆಗಳು.

ಆರ್ - ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧ

ಪ್ರತಿರೋಧವು ವೋಲ್ಟೇಜ್ನ ಪರಸ್ಪರ ಸಂಬಂಧವಾಗಿದೆ ಮತ್ತು ಹರಿಯುವ ನೀರಿನಲ್ಲಿ ಚಲನೆಯ ವಿರುದ್ಧ ದೇಹವನ್ನು ಚಲಿಸುವ ಪರಿಣಾಮಕ್ಕೆ ಹೋಲಿಸಬಹುದು. R ನ ಘಟಕವು ಓಂ ಆಗಿದೆ, ಇದನ್ನು ಕ್ಯಾಪಿಟಲ್ ಗ್ರೀಕ್ ಅಕ್ಷರ ಒಮೆಗಾದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ಪ್ರತಿರೋಧದ ಪರಸ್ಪರ (1/R) ಅನ್ನು ವಾಹಕತೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಇದು ಸೀಮೆನ್ಸ್ ಘಟಕಗಳಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಿದ ಚಾರ್ಜ್ ಅನ್ನು ನಡೆಸುವ ವಸ್ತುವಿನ ಸಾಮರ್ಥ್ಯವನ್ನು ಅಳೆಯುತ್ತದೆ.

ಬಳಸಿದ ಜ್ಯಾಮಿತೀಯವಾಗಿ ಸ್ವತಂತ್ರ ಪ್ರಮಾಣವನ್ನು ಪ್ರತಿರೋಧಕತೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಇದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಗ್ರೀಕ್ ಚಿಹ್ನೆ r ನಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ಹೆಚ್ಚುವರಿ ಮಾಹಿತಿ. ಓಮ್ನ ಕಾನೂನು ವಿದ್ಯುತ್ ಜಾಲದ ಕಾರ್ಯಾಚರಣೆಯ ಮೂರು ಪ್ರಮುಖ ಸೂಚಕಗಳನ್ನು ಸ್ಥಾಪಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ, ಇದು ಶಕ್ತಿಯ ಲೆಕ್ಕಾಚಾರವನ್ನು ಸರಳಗೊಳಿಸುತ್ತದೆ. ಡಯೋಡ್, ಟ್ರಾನ್ಸಿಸ್ಟರ್ ಮತ್ತು ಮುಂತಾದ ಅಂಶಗಳೊಂದಿಗೆ ಏಕಪಕ್ಷೀಯ ನೆಟ್ವರ್ಕ್ಗಳಿಗೆ ಇದು ಅನ್ವಯಿಸುವುದಿಲ್ಲ. ಮತ್ತು ಇದು ರೇಖಾತ್ಮಕವಲ್ಲದ ಅಂಶಗಳಿಗೆ ಅನ್ವಯಿಸುವುದಿಲ್ಲ, ಅದರಲ್ಲಿ ಥೈರಿಸ್ಟರ್‌ಗಳು ಉದಾಹರಣೆಗಳಾಗಿವೆ, ಏಕೆಂದರೆ ಈ ಅಂಶಗಳ ಪ್ರತಿರೋಧ ಮೌಲ್ಯವು ವಿಭಿನ್ನ ನೀಡಿದ ವೋಲ್ಟೇಜ್ ಮತ್ತು ಪ್ರವಾಹದೊಂದಿಗೆ ಬದಲಾಗುತ್ತದೆ.

ಹೆಚ್ಚಿನ ಆವರ್ತನಗಳಲ್ಲಿ, ವಿತರಿಸಿದ ನಡವಳಿಕೆಯು ಪ್ರಬಲವಾಗುತ್ತದೆ. ಬಹಳ ಉದ್ದವಾದ ವಿದ್ಯುತ್ ಲೈನ್‌ಗಳಲ್ಲಿ ಅದೇ ವಿಷಯ ಸಂಭವಿಸುತ್ತದೆ. 60 Hz ಗಿಂತ ಕಡಿಮೆ ಆವರ್ತನದಲ್ಲಿಯೂ ಸಹ, 30 ಕಿಮೀ ನಂತಹ ಬಹಳ ಉದ್ದವಾದ ಪ್ರಸರಣ ಮಾರ್ಗವು ವಿತರಿಸಿದ ಸ್ವಭಾವವನ್ನು ಹೊಂದಿದೆ.ಮುಖ್ಯ ಕಾರಣವೆಂದರೆ ಸರ್ಕ್ಯೂಟ್‌ಗಳಲ್ಲಿ ಹರಡುವ ಪರಿಣಾಮಕಾರಿ ವಿದ್ಯುತ್ ಸಂಕೇತಗಳು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು, ವೋಲ್ಟ್ ಮತ್ತು ಆಂಪಿಯರ್‌ಗಳಲ್ಲ, ಇದು ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದಿಂದ ಸೋಂಕಿಗೆ ಒಳಗಾಗುತ್ತದೆ. ವಾಹಕಗಳು ಅಲೆಗಳಿಗೆ ಮಾರ್ಗದರ್ಶಿಗಳಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ. ಆದ್ದರಿಂದ, ಉದಾಹರಣೆಗೆ, ಒಂದು ಏಕಾಕ್ಷ ಕೇಬಲ್ Z = 75 ಓಎಚ್ಎಮ್ಗಳನ್ನು ತೋರಿಸುತ್ತದೆ, ಅದರ DC ಪ್ರತಿರೋಧವು ಅತ್ಯಲ್ಪವಾಗಿದ್ದರೂ ಸಹ.

ಓಮ್ನ ನಿಯಮವು ಎಲೆಕ್ಟ್ರಿಕಲ್ ಇಂಜಿನಿಯರಿಂಗ್ನ ಮೂಲಭೂತ ನಿಯಮವಾಗಿದೆ. ಇದು ಎಲ್ಲಾ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳು ಮತ್ತು ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಘಟಕಗಳಲ್ಲಿ ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಪ್ರಾಯೋಗಿಕ ಅಪ್ಲಿಕೇಶನ್‌ಗಳನ್ನು ಹೊಂದಿದೆ.

ಓಮ್ಸ್ ನಿಯಮದ ಅನ್ವಯದ ಸಾಮಾನ್ಯ ಉದಾಹರಣೆಗಳು:

1. ವಿದ್ಯುತ್ ಹೀಟರ್ಗೆ ವಿದ್ಯುತ್ ಸರಬರಾಜು. ಹೀಟರ್ ಕಾಯಿಲ್ ಮತ್ತು ಅನ್ವಯಿಕ ವೋಲ್ಟೇಜ್ನ ಪ್ರತಿರೋಧವನ್ನು ನೀಡಿದರೆ, ಆ ಹೀಟರ್ಗೆ ಸರಬರಾಜು ಮಾಡಲಾದ ವಿದ್ಯುತ್ ಅನ್ನು ಲೆಕ್ಕಹಾಕಬಹುದು.
2. ಫ್ಯೂಸ್ಗಳ ಆಯ್ಕೆ. ಅವು ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಸಾಧನಗಳೊಂದಿಗೆ ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಗೊಂಡಿರುವ ರಕ್ಷಣಾ ಘಟಕಗಳಾಗಿವೆ. ಫ್ಯೂಸ್‌ಗಳು/ಸಿಬಿಗಳನ್ನು ಆಂಪ್ಸ್‌ಗಳಲ್ಲಿ ರೇಟ್ ಮಾಡಲಾಗುತ್ತದೆ. ಪ್ರಸ್ತುತ ಫ್ಯೂಸ್ ರೇಟಿಂಗ್ ಅನ್ನು ಓಮ್ನ ನಿಯಮವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ.
3. ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಸಾಧನಗಳ ವಿನ್ಯಾಸ. ಲ್ಯಾಪ್‌ಟಾಪ್‌ಗಳು ಮತ್ತು ಮೊಬೈಲ್ ಫೋನ್‌ಗಳಂತಹ ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಸಾಧನಗಳಿಗೆ ನಿರ್ದಿಷ್ಟ ಪ್ರಸ್ತುತ ರೇಟಿಂಗ್‌ನೊಂದಿಗೆ DC ವಿದ್ಯುತ್ ಸರಬರಾಜು ಅಗತ್ಯವಿರುತ್ತದೆ. ವಿಶಿಷ್ಟವಾದ ಮೊಬೈಲ್ ಫೋನ್ ಬ್ಯಾಟರಿಗಳಿಗೆ 0.7-1A ಅಗತ್ಯವಿರುತ್ತದೆ. ಈ ಘಟಕಗಳ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹದ ದರವನ್ನು ನಿಯಂತ್ರಿಸಲು ಪ್ರತಿರೋಧಕವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಓಮ್ನ ನಿಯಮವನ್ನು ವಿಶಿಷ್ಟ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ರೇಟ್ ಮಾಡಲಾದ ಪ್ರವಾಹವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಬಳಸಲಾಗುತ್ತದೆ.

ಒಂದು ಸಮಯದಲ್ಲಿ, ಓಮ್ನ ತೀರ್ಮಾನಗಳು ವಿದ್ಯುಚ್ಛಕ್ತಿ ಕ್ಷೇತ್ರದಲ್ಲಿ ಹೊಸ ಸಂಶೋಧನೆಗೆ ವೇಗವರ್ಧಕವಾಗಿ ಮಾರ್ಪಟ್ಟಿವೆ ಮತ್ತು ಇಂದು ಅವರು ತಮ್ಮ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಕಳೆದುಕೊಂಡಿಲ್ಲ, ಏಕೆಂದರೆ ಆಧುನಿಕ ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್ ಅವುಗಳ ಮೇಲೆ ಆಧಾರಿತವಾಗಿದೆ. 1841 ರಲ್ಲಿ, ಓಂ ಅವರಿಗೆ ರಾಯಲ್ ಸೊಸೈಟಿಯ ಅತ್ಯುನ್ನತ ಗೌರವವಾದ ಕಾಪ್ಲೆ ಪದಕವನ್ನು ನೀಡಲಾಯಿತು ಮತ್ತು "ಓಂ" ಪದವನ್ನು 1872 ರ ಹಿಂದೆಯೇ ಪ್ರತಿರೋಧದ ಘಟಕವಾಗಿ ಗುರುತಿಸಲಾಯಿತು.

ಡಿಸಿ ಸರ್ಕ್ಯೂಟ್ನ ಏಕರೂಪವಲ್ಲದ ವಿಭಾಗ

ಒಂದು ವೈವಿಧ್ಯಮಯ ರಚನೆಯು ಸರ್ಕ್ಯೂಟ್ನ ಅಂತಹ ವಿಭಾಗವನ್ನು ಹೊಂದಿದೆ, ಅಲ್ಲಿ ವಾಹಕಗಳು ಮತ್ತು ಅಂಶಗಳ ಜೊತೆಗೆ, ಪ್ರಸ್ತುತ ಮೂಲವಿದೆ. ಈ ಪ್ರದೇಶದಲ್ಲಿ ಒಟ್ಟು ಪ್ರಸ್ತುತ ಶಕ್ತಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ ಅದರ EMF ಅನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು.

ವೈವಿಧ್ಯಮಯ ಸೈಟ್‌ನ ಮುಖ್ಯ ನಿಯತಾಂಕಗಳು ಮತ್ತು ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವ ಒಂದು ಸೂತ್ರವಿದೆ: q = q0 x n x V. ಅದರ ಸೂಚಕಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ನಿರೂಪಿಸಲಾಗಿದೆ:

• ಚಲಿಸುವ ಶುಲ್ಕಗಳ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ (q), ಅವರು ನಿರ್ದಿಷ್ಟ ಸಾಂದ್ರತೆಯನ್ನು ಪಡೆದುಕೊಳ್ಳುತ್ತಾರೆ. ಇದರ ಕಾರ್ಯಕ್ಷಮತೆ ಪ್ರಸ್ತುತ ಶಕ್ತಿ ಮತ್ತು ಕಂಡಕ್ಟರ್ (ಎಸ್) ನ ಅಡ್ಡ-ವಿಭಾಗದ ಪ್ರದೇಶವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.
• ನಿರ್ದಿಷ್ಟ ಸಾಂದ್ರತೆಯ (n) ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ, ಒಂದೇ ಅವಧಿಯಲ್ಲಿ ಚಲಿಸಿದ ಯುನಿಟ್ ಶುಲ್ಕಗಳ (q0) ಸಂಖ್ಯೆಯನ್ನು ನಿಖರವಾಗಿ ಸೂಚಿಸಲು ಸಾಧ್ಯವಿದೆ.
• ಲೆಕ್ಕಾಚಾರಗಳಿಗಾಗಿ, ಕಂಡಕ್ಟರ್ ಅನ್ನು ಷರತ್ತುಬದ್ಧವಾಗಿ ಕೆಲವು ಪರಿಮಾಣದೊಂದಿಗೆ (ವಿ) ಸಿಲಿಂಡರಾಕಾರದ ವಿಭಾಗವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ.

ಕಂಡಕ್ಟರ್ ಅನ್ನು ಬ್ಯಾಟರಿಗೆ ಸಂಪರ್ಕಿಸುವಾಗ, ಸ್ವಲ್ಪ ಸಮಯದ ನಂತರ ಎರಡನೆಯದು ಬಿಡುಗಡೆಯಾಗುತ್ತದೆ. ಅಂದರೆ, ಎಲೆಕ್ಟ್ರಾನ್ಗಳ ಚಲನೆಯು ಕ್ರಮೇಣ ನಿಧಾನಗೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಕೊನೆಯಲ್ಲಿ, ಸಂಪೂರ್ಣವಾಗಿ ನಿಲ್ಲುತ್ತದೆ. ವಾಹಕದ ಆಣ್ವಿಕ ಜಾಲರಿಯಿಂದ ಇದನ್ನು ಸುಗಮಗೊಳಿಸಲಾಗುತ್ತದೆ, ಇದು ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಘರ್ಷಣೆಯನ್ನು ಪರಸ್ಪರ ಮತ್ತು ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಪ್ರತಿರೋಧಿಸುತ್ತದೆ. ಅಂತಹ ಪ್ರತಿರೋಧವನ್ನು ಜಯಿಸಲು, ಕೆಲವು ತೃತೀಯ ಶಕ್ತಿಗಳನ್ನು ಹೆಚ್ಚುವರಿಯಾಗಿ ಅನ್ವಯಿಸಬೇಕು.

ಲೆಕ್ಕಾಚಾರದ ಸಮಯದಲ್ಲಿ, ಈ ಬಲಗಳನ್ನು ಕೂಲಂಬ್ ಪದಗಳಿಗಿಂತ ಸೇರಿಸಲಾಗುತ್ತದೆ. ಹೆಚ್ಚುವರಿಯಾಗಿ, ಯುನಿಟ್ ಚಾರ್ಜ್ q ಅನ್ನು 1 ನೇ ಬಿಂದುವಿನಿಂದ 2 ನೇ ಸ್ಥಾನಕ್ಕೆ ವರ್ಗಾಯಿಸಲು, A1-2 ಅಥವಾ ಸರಳವಾಗಿ A12 ಕೆಲಸವನ್ನು ನಿರ್ವಹಿಸುವುದು ಅಗತ್ಯವಾಗಿರುತ್ತದೆ. ಈ ಉದ್ದೇಶಕ್ಕಾಗಿ, ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವನ್ನು (ϕ1 - ϕ2) ರಚಿಸಲಾಗಿದೆ. ನೇರ ಪ್ರವಾಹದ ಮೂಲದ ಕ್ರಿಯೆಯ ಅಡಿಯಲ್ಲಿ, ಇಎಮ್ಎಫ್ ಉದ್ಭವಿಸುತ್ತದೆ, ಸರ್ಕ್ಯೂಟ್ ಉದ್ದಕ್ಕೂ ಚಲಿಸುವ ಶುಲ್ಕಗಳು. ಒಟ್ಟು ಒತ್ತಡದ ಪ್ರಮಾಣವು ಮೇಲೆ ತಿಳಿಸಿದ ಎಲ್ಲಾ ಬಲಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ.

ಡಿಸಿ ಪೂರೈಕೆಗೆ ಸಂಪರ್ಕದ ಧ್ರುವೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಟರ್ಮಿನಲ್‌ಗಳನ್ನು ಬದಲಾಯಿಸಿದಾಗ, EMF ಸಹ ಬದಲಾಗುತ್ತದೆ, ಶುಲ್ಕಗಳ ಚಲನೆಯನ್ನು ವೇಗಗೊಳಿಸುತ್ತದೆ ಅಥವಾ ನಿಧಾನಗೊಳಿಸುತ್ತದೆ.

ಅಂಶಗಳ ಸರಣಿ ಮತ್ತು ಸಮಾನಾಂತರ ಸಂಪರ್ಕ

ಎಲೆಕ್ಟ್ರಿಕಲ್ ಸರ್ಕ್ಯೂಟ್ನ ಅಂಶಗಳಿಗೆ (ಸರ್ಕ್ಯೂಟ್ನ ವಿಭಾಗ), ವಿಶಿಷ್ಟ ಕ್ಷಣವು ಸರಣಿ ಅಥವಾ ಸಮಾನಾಂತರ ಸಂಪರ್ಕವಾಗಿದೆ.

ಅಂತೆಯೇ, ಪ್ರತಿಯೊಂದು ರೀತಿಯ ಸಂಪರ್ಕವು ಪ್ರಸ್ತುತ ಹರಿವು ಮತ್ತು ವೋಲ್ಟೇಜ್ ಪೂರೈಕೆಯ ವಿಭಿನ್ನ ಸ್ವಭಾವದೊಂದಿಗೆ ಇರುತ್ತದೆ. ಈ ಖಾತೆಯಲ್ಲಿ, ಅಂಶಗಳನ್ನು ಸೇರಿಸುವ ಆಯ್ಕೆಯನ್ನು ಅವಲಂಬಿಸಿ ಓಮ್‌ನ ನಿಯಮವನ್ನು ವಿವಿಧ ರೀತಿಯಲ್ಲಿ ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ.

ಸರಣಿ-ಸಂಪರ್ಕಿತ ಪ್ರತಿರೋಧಕ ಅಂಶಗಳ ಸರಣಿ

ಸರಣಿ ಸಂಪರ್ಕಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ (ಎರಡು ಘಟಕಗಳೊಂದಿಗೆ ಸರ್ಕ್ಯೂಟ್ನ ವಿಭಾಗ), ಪದಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ:

• I = I₁ = I₂ ;
• ಯು = ಯು₁ + ಯು₂ ;
• ಆರ್=ಆರ್₁ + ಆರ್₂

ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಗೊಂಡಿರುವ ಪ್ರತಿರೋಧಕ ಘಟಕಗಳ ಸಂಖ್ಯೆಯನ್ನು ಲೆಕ್ಕಿಸದೆಯೇ, ಸರ್ಕ್ಯೂಟ್ನ ಒಂದು ವಿಭಾಗದಲ್ಲಿ ಹರಿಯುವ ಪ್ರವಾಹವು ಮೌಲ್ಯವನ್ನು ಬದಲಾಯಿಸುವುದಿಲ್ಲ ಎಂದು ಈ ಸೂತ್ರೀಕರಣವು ಸ್ಪಷ್ಟವಾಗಿ ತೋರಿಸುತ್ತದೆ.

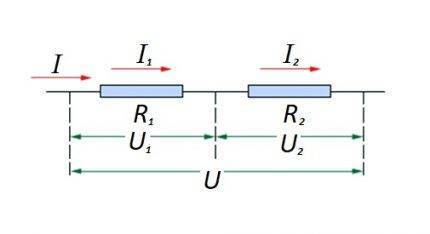ಸರಣಿಯಲ್ಲಿ ಸರ್ಕ್ಯೂಟ್ ವಿಭಾಗದಲ್ಲಿ ಪ್ರತಿರೋಧಕ ಅಂಶಗಳನ್ನು ಪರಸ್ಪರ ಸಂಪರ್ಕಿಸುವುದು. ಈ ಆಯ್ಕೆಯು ತನ್ನದೇ ಆದ ಲೆಕ್ಕಾಚಾರದ ಕಾನೂನನ್ನು ಹೊಂದಿದೆ. ರೇಖಾಚಿತ್ರದಲ್ಲಿ: I, I1, I2 - ಪ್ರಸ್ತುತ ಹರಿವು; R1, R2 - ಪ್ರತಿರೋಧಕ ಅಂಶಗಳು; U, U1, U2 - ಅನ್ವಯಿಕ ವೋಲ್ಟೇಜ್

ಸರ್ಕ್ಯೂಟ್ನ ಸಕ್ರಿಯ ನಿರೋಧಕ ಘಟಕಗಳಿಗೆ ಅನ್ವಯಿಸಲಾದ ವೋಲ್ಟೇಜ್ ಮೊತ್ತವು ಮೊತ್ತವಾಗಿದೆ ಮತ್ತು EMF ಮೂಲದ ಮೌಲ್ಯಕ್ಕೆ ಸೇರಿಸುತ್ತದೆ.

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರತಿಯೊಂದು ಘಟಕದ ಮೇಲಿನ ವೋಲ್ಟೇಜ್: Ux = I * Rx.

ಒಟ್ಟು ಪ್ರತಿರೋಧವನ್ನು ಸರ್ಕ್ಯೂಟ್ನ ಎಲ್ಲಾ ಪ್ರತಿರೋಧಕ ಘಟಕಗಳ ಮೌಲ್ಯಗಳ ಮೊತ್ತವೆಂದು ಪರಿಗಣಿಸಬೇಕು.

ಸಮಾನಾಂತರ ಸಂಪರ್ಕಿತ ಪ್ರತಿರೋಧಕ ಅಂಶಗಳ ಸರಪಳಿ

ಪ್ರತಿರೋಧಕ ಘಟಕಗಳ ಸಮಾನಾಂತರ ಸಂಪರ್ಕವಿರುವ ಸಂದರ್ಭದಲ್ಲಿ, ಜರ್ಮನ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಓಮ್ನ ನಿಯಮಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಸೂತ್ರೀಕರಣವನ್ನು ನ್ಯಾಯೋಚಿತವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ:

• I = I₁ + ಐ₂ … ;
• ಯು = ಯು₁ = ಯು₂ … ;
• 1/ಆರ್ = 1/ಆರ್₁ + 1 / ಆರ್₂ + …

ಸಮಾನಾಂತರ ಮತ್ತು ಸರಣಿ ಸಂಪರ್ಕಗಳನ್ನು ಬಳಸಿದಾಗ "ಮಿಶ್ರ" ಪ್ರಕಾರದ ಸರ್ಕ್ಯೂಟ್ ವಿಭಾಗಗಳನ್ನು ಕಂಪೈಲ್ ಮಾಡುವ ಆಯ್ಕೆಗಳನ್ನು ಹೊರಗಿಡಲಾಗುವುದಿಲ್ಲ.

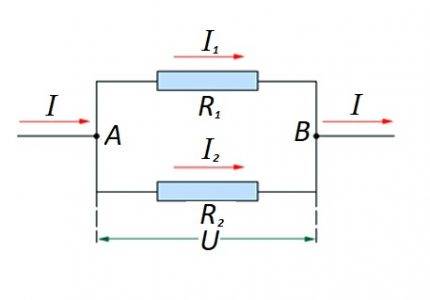ಪರಸ್ಪರ ಸಮಾನಾಂತರವಾಗಿ ಸರ್ಕ್ಯೂಟ್ ವಿಭಾಗದಲ್ಲಿ ಪ್ರತಿರೋಧಕ ಅಂಶಗಳ ಸಂಪರ್ಕ. ಈ ಆಯ್ಕೆಗಾಗಿ, ತನ್ನದೇ ಆದ ಲೆಕ್ಕಾಚಾರದ ಕಾನೂನನ್ನು ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ. ರೇಖಾಚಿತ್ರದಲ್ಲಿ: I, I1, I2 - ಪ್ರಸ್ತುತ ಹರಿವು; R1, R2 - ಪ್ರತಿರೋಧಕ ಅಂಶಗಳು; ಯು - ಅನ್ವಯಿಕ ವೋಲ್ಟೇಜ್; ಎ, ಬಿ - ಪ್ರವೇಶ / ನಿರ್ಗಮನ ಬಿಂದುಗಳು

ಅಂತಹ ಆಯ್ಕೆಗಳಿಗಾಗಿ, ಸಮಾನಾಂತರ ಸಂಪರ್ಕದ ಪ್ರತಿರೋಧಕ ರೇಟಿಂಗ್ನ ಆರಂಭಿಕ ಲೆಕ್ಕಾಚಾರದಿಂದ ಸಾಮಾನ್ಯವಾಗಿ ಲೆಕ್ಕಾಚಾರವನ್ನು ಕೈಗೊಳ್ಳಲಾಗುತ್ತದೆ. ನಂತರ ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಗೊಂಡಿರುವ ಪ್ರತಿರೋಧಕದ ಮೌಲ್ಯವನ್ನು ಫಲಿತಾಂಶಕ್ಕೆ ಸೇರಿಸಲಾಗುತ್ತದೆ.

ಕಾನೂನಿನ ಅವಿಭಾಜ್ಯ ಮತ್ತು ಭೇದಾತ್ಮಕ ರೂಪಗಳು

ಲೆಕ್ಕಾಚಾರಗಳೊಂದಿಗೆ ಮೇಲಿನ ಎಲ್ಲಾ ಅಂಶಗಳು "ಏಕರೂಪದ" ರಚನೆಯ ವಾಹಕಗಳನ್ನು ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ಗಳ ಭಾಗವಾಗಿ ಬಳಸಿದಾಗ ಪರಿಸ್ಥಿತಿಗಳಿಗೆ ಅನ್ವಯಿಸುತ್ತವೆ.

ಏತನ್ಮಧ್ಯೆ, ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಒಂದು ಸ್ಕೀಮ್ಯಾಟಿಕ್ ನಿರ್ಮಾಣವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಎದುರಿಸಬೇಕಾಗುತ್ತದೆ, ಅಲ್ಲಿ ವಾಹಕಗಳ ರಚನೆಯು ವಿವಿಧ ಪ್ರದೇಶಗಳಲ್ಲಿ ಬದಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ದೊಡ್ಡ ಅಡ್ಡ ವಿಭಾಗದ ತಂತಿಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ ಅಥವಾ ಇದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ವಿಭಿನ್ನ ವಸ್ತುಗಳ ಆಧಾರದ ಮೇಲೆ ಚಿಕ್ಕದಾಗಿದೆ.

ಅಂತಹ ವ್ಯತ್ಯಾಸಗಳನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಲು, "ಡಿಫರೆನ್ಷಿಯಲ್-ಅವಿಭಾಜ್ಯ ಓಮ್ನ ನಿಯಮ" ಎಂದು ಕರೆಯಲ್ಪಡುವ ವ್ಯತ್ಯಾಸವಿದೆ. ಅಪರಿಮಿತ ಸಣ್ಣ ವಾಹಕಕ್ಕಾಗಿ, ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯ ಮಟ್ಟವನ್ನು ತೀವ್ರತೆ ಮತ್ತು ವಾಹಕತೆಯ ಮೌಲ್ಯವನ್ನು ಅವಲಂಬಿಸಿ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ.

ವಿಭಿನ್ನ ಲೆಕ್ಕಾಚಾರದ ಅಡಿಯಲ್ಲಿ, ಸೂತ್ರವನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ: J = ό * E

ಸಮಗ್ರ ಲೆಕ್ಕಾಚಾರಕ್ಕಾಗಿ, ಅನುಕ್ರಮವಾಗಿ, ಸೂತ್ರೀಕರಣ: I * R = φ1 - φ2 + έ

ಆದಾಗ್ಯೂ, ಈ ಉದಾಹರಣೆಗಳು ಉನ್ನತ ಗಣಿತಶಾಸ್ತ್ರದ ಶಾಲೆಗೆ ಹತ್ತಿರದಲ್ಲಿವೆ ಮತ್ತು ಸರಳ ಎಲೆಕ್ಟ್ರಿಷಿಯನ್‌ನ ನೈಜ ಅಭ್ಯಾಸದಲ್ಲಿ ವಾಸ್ತವವಾಗಿ ಬಳಸಲಾಗುವುದಿಲ್ಲ.

ಪ್ರಸ್ತುತ ಮತ್ತು ಪ್ರತಿರೋಧವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು

ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಪರಿಕಲ್ಪನೆಯೊಂದಿಗೆ ಪ್ರಾರಂಭಿಸೋಣ.ಸಂಕ್ಷಿಪ್ತವಾಗಿ, ಲೋಹಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಎಲೆಕ್ಟ್ರಾನ್ಗಳ ನಿರ್ದೇಶನದ ಚಲನೆಯಾಗಿದೆ - ಋಣಾತ್ಮಕ ಆವೇಶದ ಕಣಗಳು. ಅವುಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸಣ್ಣ ವಲಯಗಳಾಗಿ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ. ಶಾಂತ ಸ್ಥಿತಿಯಲ್ಲಿ, ಅವರು ಅಸ್ತವ್ಯಸ್ತವಾಗಿ ಚಲಿಸುತ್ತಾರೆ, ನಿರಂತರವಾಗಿ ತಮ್ಮ ದಿಕ್ಕನ್ನು ಬದಲಾಯಿಸುತ್ತಾರೆ. ಕೆಲವು ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ - ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸದ ನೋಟ - ಈ ಕಣಗಳು ಕೆಲವು ದಿಕ್ಕಿನಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಚಲನೆಯನ್ನು ಪ್ರಾರಂಭಿಸುತ್ತವೆ. ಈ ಚಲನೆಯು ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿದೆ.

ಅದನ್ನು ಸ್ಪಷ್ಟಪಡಿಸಲು, ನಾವು ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳನ್ನು ಕೆಲವು ಸಮತಲದಲ್ಲಿ ಚೆಲ್ಲಿದ ನೀರಿನಿಂದ ಹೋಲಿಸಬಹುದು. ವಿಮಾನವು ಸ್ಥಿರವಾಗಿರುವವರೆಗೆ, ನೀರು ಚಲಿಸುವುದಿಲ್ಲ. ಆದರೆ, ಇಳಿಜಾರು ಕಾಣಿಸಿಕೊಂಡ ತಕ್ಷಣ (ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು ಹುಟ್ಟಿಕೊಂಡಿತು), ನೀರು ಚಲಿಸಲು ಪ್ರಾರಂಭಿಸಿತು. ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ವಿಷಯದಲ್ಲೂ ಅಷ್ಟೇ.

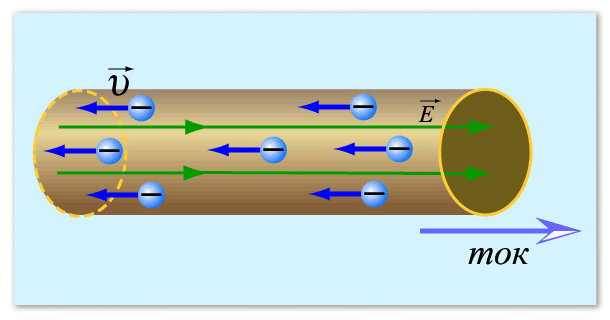
ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ಈ ರೀತಿ ಕಲ್ಪಿಸಿಕೊಳ್ಳಬಹುದು

ಈಗ ನಾವು ಪ್ರತಿರೋಧವನ್ನು ಏನೆಂದು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬೇಕು ಮತ್ತು ಅವರು ಪ್ರಸ್ತುತ ಶಕ್ತಿಯೊಂದಿಗೆ ಪ್ರತಿಕ್ರಿಯೆಯನ್ನು ಏಕೆ ಹೊಂದಿದ್ದಾರೆ: ಹೆಚ್ಚಿನ ಪ್ರತಿರೋಧ, ಕಡಿಮೆ ಪ್ರಸ್ತುತ. ನಿಮಗೆ ತಿಳಿದಿರುವಂತೆ, ಎಲೆಕ್ಟ್ರಾನ್ಗಳು ವಾಹಕದ ಮೂಲಕ ಚಲಿಸುತ್ತವೆ. ಸಾಮಾನ್ಯವಾಗಿ ಇವು ಲೋಹದ ತಂತಿಗಳಾಗಿವೆ, ಏಕೆಂದರೆ ಲೋಹಗಳು ವಿದ್ಯುತ್ ಅನ್ನು ನಡೆಸುವ ಉತ್ತಮ ಸಾಮರ್ಥ್ಯವನ್ನು ಹೊಂದಿವೆ. ಲೋಹವು ದಟ್ಟವಾದ ಸ್ಫಟಿಕ ಜಾಲರಿಯನ್ನು ಹೊಂದಿದೆ ಎಂದು ನಮಗೆ ತಿಳಿದಿದೆ: ಹತ್ತಿರ ಮತ್ತು ಪರಸ್ಪರ ಸಂಪರ್ಕ ಹೊಂದಿರುವ ಅನೇಕ ಕಣಗಳು. ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು, ಲೋಹದ ಪರಮಾಣುಗಳ ನಡುವೆ ತಮ್ಮ ಮಾರ್ಗವನ್ನು ಮಾಡುತ್ತವೆ, ಅವುಗಳೊಂದಿಗೆ ಡಿಕ್ಕಿಹೊಡೆಯುತ್ತವೆ, ಇದು ಚಲಿಸಲು ಕಷ್ಟವಾಗುತ್ತದೆ. ವಾಹಕದ ಪ್ರತಿರೋಧವನ್ನು ವಿವರಿಸಲು ಇದು ಸಹಾಯ ಮಾಡುತ್ತದೆ. ಈಗ ಅದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ ಏಕೆ ಹೆಚ್ಚಿನ ಪ್ರತಿರೋಧ, ಕಡಿಮೆ ಪ್ರಸ್ತುತ ಶಕ್ತಿ - ಹೆಚ್ಚು ಕಣಗಳು, ಎಲೆಕ್ಟ್ರಾನ್ಗಳು ಮಾರ್ಗವನ್ನು ಜಯಿಸಲು ಹೆಚ್ಚು ಕಷ್ಟ, ಅವರು ಅದನ್ನು ಹೆಚ್ಚು ನಿಧಾನವಾಗಿ ಮಾಡುತ್ತಾರೆ. ಇದನ್ನು ವಿಂಗಡಿಸಲಾಗಿದೆ ಎಂದು ತೋರುತ್ತದೆ.

ಈ ಅವಲಂಬನೆಯನ್ನು ಪ್ರಾಯೋಗಿಕವಾಗಿ ಪರೀಕ್ಷಿಸಲು ನೀವು ಬಯಸಿದರೆ, ವೇರಿಯಬಲ್ ರೆಸಿಸ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ, ಸರಣಿಯಲ್ಲಿ ರೆಸಿಸ್ಟರ್ ಅನ್ನು ಸಂಪರ್ಕಿಸಿ - ಆಮ್ಮೀಟರ್ - ಪ್ರಸ್ತುತ ಮೂಲ (ಬ್ಯಾಟರಿ).ಸರ್ಕ್ಯೂಟ್ಗೆ ಸ್ವಿಚ್ ಅನ್ನು ಸೇರಿಸಲು ಸಹ ಅಪೇಕ್ಷಣೀಯವಾಗಿದೆ - ಸಾಮಾನ್ಯ ಟಾಗಲ್ ಸ್ವಿಚ್.

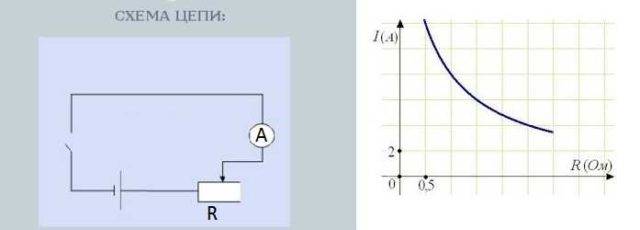
ಪ್ರತಿರೋಧದ ಮೇಲೆ ಪ್ರವಾಹದ ಅವಲಂಬನೆಯನ್ನು ಪರೀಕ್ಷಿಸಲು ಸರ್ಕ್ಯೂಟ್

ರೆಸಿಸ್ಟರ್ ನಾಬ್ ಅನ್ನು ತಿರುಗಿಸುವುದು ಪ್ರತಿರೋಧವನ್ನು ಬದಲಾಯಿಸುತ್ತದೆ. ಅದೇ ಸಮಯದಲ್ಲಿ, ಪ್ರಸ್ತುತ ಶಕ್ತಿಯನ್ನು ಅಳೆಯುವ ಆಮ್ಮೀಟರ್ನಲ್ಲಿನ ವಾಚನಗೋಷ್ಠಿಗಳು ಸಹ ಬದಲಾಗುತ್ತವೆ. ಇದಲ್ಲದೆ, ಹೆಚ್ಚಿನ ಪ್ರತಿರೋಧ, ಕಡಿಮೆ ಬಾಣದ ವಿಚಲನ - ಕಡಿಮೆ ಪ್ರಸ್ತುತ. ಕಡಿಮೆ ಪ್ರತಿರೋಧ, ಬಾಣವು ಹೆಚ್ಚು ವಿಚಲನಗೊಳ್ಳುತ್ತದೆ - ಪ್ರಸ್ತುತವು ಹೆಚ್ಚಾಗಿರುತ್ತದೆ.

ಪ್ರತಿರೋಧದ ಮೇಲಿನ ಪ್ರವಾಹದ ಅವಲಂಬನೆಯು ಬಹುತೇಕ ರೇಖೀಯವಾಗಿದೆ, ಅಂದರೆ, ಇದು ಗ್ರಾಫ್ನಲ್ಲಿ ಬಹುತೇಕ ಸರಳ ರೇಖೆಯಂತೆ ಪ್ರತಿಫಲಿಸುತ್ತದೆ. ಏಕೆ ಬಹುತೇಕ - ಇದನ್ನು ಪ್ರತ್ಯೇಕವಾಗಿ ಚರ್ಚಿಸಬೇಕು, ಆದರೆ ಅದು ಇನ್ನೊಂದು ಕಥೆ.

ಪರ್ಯಾಯ ಪ್ರವಾಹಕ್ಕೆ ಓಮ್ನ ನಿಯಮ

ಎಸಿ ಸರ್ಕ್ಯೂಟ್ಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ, ಪ್ರತಿರೋಧದ ಪರಿಕಲ್ಪನೆಯ ಬದಲಿಗೆ, "ಪ್ರತಿರೋಧ" ಎಂಬ ಪರಿಕಲ್ಪನೆಯನ್ನು ಪರಿಚಯಿಸಲಾಗಿದೆ. ಪ್ರತಿರೋಧವನ್ನು Z ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಇದು ಲೋಡ್ R ನ ಸಕ್ರಿಯ ಪ್ರತಿರೋಧವನ್ನು ಒಳಗೊಂಡಿದೆ_ಎ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕತೆ ಎಕ್ಸ್ (ಅಥವಾ ಆರ್_ಆರ್) ಇದು ಸೈನುಸೈಡಲ್ ಪ್ರವಾಹದ ಆಕಾರ (ಮತ್ತು ಯಾವುದೇ ಇತರ ರೂಪಗಳ ಪ್ರವಾಹಗಳು) ಮತ್ತು ಅನುಗಮನದ ಅಂಶಗಳ ನಿಯತಾಂಕಗಳು ಮತ್ತು ಸ್ವಿಚಿಂಗ್ ಕಾನೂನುಗಳ ಕಾರಣದಿಂದಾಗಿರುತ್ತದೆ:

1. ಇಂಡಕ್ಟಿವ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ಪ್ರವಾಹವು ತಕ್ಷಣವೇ ಬದಲಾಗುವುದಿಲ್ಲ.
2. ಕೆಪಾಸಿಟನ್ಸ್ ಹೊಂದಿರುವ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ವೋಲ್ಟೇಜ್ ತಕ್ಷಣವೇ ಬದಲಾಗುವುದಿಲ್ಲ.

ಹೀಗಾಗಿ, ಪ್ರಸ್ತುತವು ವೋಲ್ಟೇಜ್ ಅನ್ನು ವಿಳಂಬಗೊಳಿಸಲು ಅಥವಾ ಮುನ್ನಡೆಸಲು ಪ್ರಾರಂಭವಾಗುತ್ತದೆ, ಮತ್ತು ಸ್ಪಷ್ಟವಾದ ಶಕ್ತಿಯನ್ನು ಸಕ್ರಿಯ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕವಾಗಿ ವಿಂಗಡಿಸಲಾಗಿದೆ.

U=I/Z

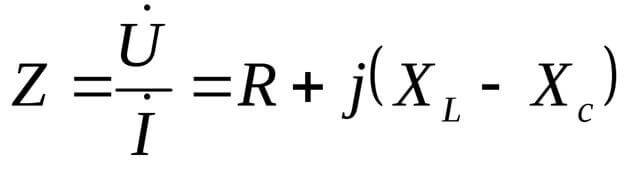
X_ಎಲ್ ಮತ್ತು ಎಕ್ಸ್_ಸಿ ಲೋಡ್ನ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಅಂಶಗಳಾಗಿವೆ.

ಈ ನಿಟ್ಟಿನಲ್ಲಿ, cosФ ಮೌಲ್ಯವನ್ನು ಪರಿಚಯಿಸಲಾಗಿದೆ:

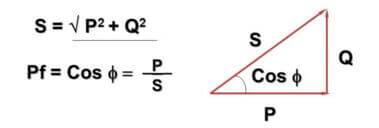
ಇಲ್ಲಿ - Q - ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಮತ್ತು ಅನುಗಮನದ-ಕೆಪ್ಯಾಸಿಟಿವ್ ಘಟಕಗಳ ಕಾರಣದಿಂದ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಶಕ್ತಿ, P - ಸಕ್ರಿಯ ಶಕ್ತಿ (ಸಕ್ರಿಯ ಘಟಕಗಳಲ್ಲಿ ಕರಗುತ್ತದೆ), S - ಸ್ಪಷ್ಟ ಶಕ್ತಿ, cosФ - ವಿದ್ಯುತ್ ಅಂಶ.

ಸೂತ್ರ ಮತ್ತು ಅದರ ಪ್ರಾತಿನಿಧ್ಯವು ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯದೊಂದಿಗೆ ಛೇದಿಸುವುದನ್ನು ನೀವು ಗಮನಿಸಿರಬಹುದು. ಇದು ನಿಜ ಮತ್ತು ಕೋನ Ф ಲೋಡ್ನ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಘಟಕವು ಎಷ್ಟು ದೊಡ್ಡದಾಗಿದೆ ಎಂಬುದರ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ - ಅದು ದೊಡ್ಡದಾಗಿದೆ, ಅದು ದೊಡ್ಡದಾಗಿದೆ.ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಇದು ವಾಸ್ತವವಾಗಿ ನೆಟ್ವರ್ಕ್ನಲ್ಲಿ ಹರಿಯುವ ಪ್ರಸ್ತುತವು ಮನೆಯ ಮೀಟರ್ನಿಂದ ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವುದಕ್ಕಿಂತ ಹೆಚ್ಚಿನದಾಗಿದೆ ಎಂಬ ಅಂಶಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ, ಆದರೆ ಉದ್ಯಮಗಳು ಪೂರ್ಣ ಶಕ್ತಿಗಾಗಿ ಪಾವತಿಸುತ್ತವೆ.

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರತಿರೋಧವನ್ನು ಸಂಕೀರ್ಣ ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸಲಾಗುತ್ತದೆ:

ಇಲ್ಲಿ j ಒಂದು ಕಾಲ್ಪನಿಕ ಘಟಕವಾಗಿದೆ, ಇದು ಸಮೀಕರಣಗಳ ಸಂಕೀರ್ಣ ರೂಪಕ್ಕೆ ವಿಶಿಷ್ಟವಾಗಿದೆ. ಕಡಿಮೆ ಸಾಮಾನ್ಯವಾಗಿ i ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಆದರೆ ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್‌ನಲ್ಲಿ, ಪರ್ಯಾಯ ಪ್ರವಾಹದ ಪರಿಣಾಮಕಾರಿ ಮೌಲ್ಯವನ್ನು ಸಹ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಆದ್ದರಿಂದ, ಗೊಂದಲಕ್ಕೀಡಾಗದಿರಲು, j ಅನ್ನು ಬಳಸುವುದು ಉತ್ತಮ.

ಕಾಲ್ಪನಿಕ ಘಟಕವು √-1 ಆಗಿದೆ. ಸ್ಕ್ವೇರ್ ಮಾಡುವಾಗ ಅಂತಹ ಸಂಖ್ಯೆ ಇಲ್ಲ ಎಂಬುದು ತಾರ್ಕಿಕವಾಗಿದೆ, ಇದು "-1" ನ ಋಣಾತ್ಮಕ ಫಲಿತಾಂಶಕ್ಕೆ ಕಾರಣವಾಗಬಹುದು.

ಓಮ್ನ ನಿಯಮ ಸಂಭವಿಸಿದಾಗ

ಆದರ್ಶ ಪರಿಸ್ಥಿತಿಗಳನ್ನು ರಚಿಸುವುದು ಸುಲಭವಲ್ಲ. ಶುದ್ಧ ವಾಹಕಗಳಲ್ಲಿಯೂ ಸಹ, ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧವು ತಾಪಮಾನದೊಂದಿಗೆ ಬದಲಾಗುತ್ತದೆ. ಅದರ ಇಳಿಕೆಯು ಸ್ಫಟಿಕ ಜಾಲರಿಯ ಅಣುಗಳ ಚಟುವಟಿಕೆಯನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ, ಇದು ಉಚಿತ ಶುಲ್ಕಗಳ ಚಲನೆಯನ್ನು ಸರಳಗೊಳಿಸುತ್ತದೆ. "ಘನೀಕರಿಸುವ" ಒಂದು ನಿರ್ದಿಷ್ಟ ಮಟ್ಟದಲ್ಲಿ ಸೂಪರ್ ಕಂಡಕ್ಟಿವಿಟಿ ಪರಿಣಾಮವು ಸಂಭವಿಸುತ್ತದೆ. ಬಿಸಿಮಾಡಿದಾಗ ವಿರುದ್ಧ ಪರಿಣಾಮವನ್ನು (ವಾಹಕತೆಯ ಕ್ಷೀಣತೆ) ಗಮನಿಸಬಹುದು.

ಅದೇ ಸಮಯದಲ್ಲಿ, ವಿದ್ಯುದ್ವಿಚ್ಛೇದ್ಯಗಳು, ಲೋಹಗಳು ಮತ್ತು ಕೆಲವು ರೀತಿಯ ಸೆರಾಮಿಕ್ಸ್ ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯನ್ನು ಲೆಕ್ಕಿಸದೆ ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧವನ್ನು ಉಳಿಸಿಕೊಳ್ಳುತ್ತವೆ. ನಿರ್ದಿಷ್ಟ ತಾಪಮಾನದ ಆಡಳಿತವನ್ನು ನಿರ್ವಹಿಸುವಾಗ ನಿಯತಾಂಕಗಳ ಸ್ಥಿರತೆಯು ಹೆಚ್ಚುವರಿ ತಿದ್ದುಪಡಿಗಳಿಲ್ಲದೆ ಓಮ್ನ ಕಾನೂನಿನ ಸೂತ್ರಗಳನ್ನು ಅನ್ವಯಿಸಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ.

ಸೆಮಿಕಂಡಕ್ಟರ್ ವಸ್ತುಗಳು ಮತ್ತು ಅನಿಲಗಳನ್ನು ವಿವಿಧ ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧದಿಂದ ನಿರೂಪಿಸಲಾಗಿದೆ. ನಿಯಂತ್ರಣ ಪರಿಮಾಣದಲ್ಲಿನ ಪ್ರಸ್ತುತ ತೀವ್ರತೆಯಿಂದ ಈ ನಿಯತಾಂಕವು ಗಮನಾರ್ಹವಾಗಿ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ. ಕಾರ್ಯಕ್ಷಮತೆಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ವಿಶೇಷ ಲೆಕ್ಕಾಚಾರದ ವಿಧಾನಗಳನ್ನು ಅನ್ವಯಿಸಬೇಕು.

ಪರ್ಯಾಯ ಪ್ರವಾಹವನ್ನು ಪರಿಗಣಿಸಿದರೆ, ಲೆಕ್ಕಾಚಾರದ ವಿಧಾನವನ್ನು ಸರಿಪಡಿಸಲಾಗುತ್ತದೆ.ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಘಟಕಗಳ ಉಪಸ್ಥಿತಿಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕಾಗುತ್ತದೆ. ಪ್ರತಿರೋಧದ ಪ್ರತಿರೋಧಕ ಸ್ವಭಾವದೊಂದಿಗೆ, ಓಮ್ನ ನಿಯಮದ ಸೂತ್ರಗಳ ಆಧಾರದ ಮೇಲೆ ಪರಿಗಣಿಸಲಾದ ಲೆಕ್ಕಾಚಾರದ ತಂತ್ರಜ್ಞಾನಗಳನ್ನು ಅನ್ವಯಿಸಲು ಸಾಧ್ಯವಿದೆ.

ಕಿರ್ಚಾಫ್ ಕಾನೂನುಗಳು.

ವಿತರಣೆ
ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಶಾಖೆಗಳಲ್ಲಿ ಪ್ರವಾಹಗಳು
ಕಿರ್ಚಾಫ್‌ನ ಮೊದಲ ನಿಯಮವನ್ನು ಪಾಲಿಸುತ್ತಾನೆ,
ಮತ್ತು ವಿಭಾಗಗಳ ಮೇಲೆ ಒತ್ತಡಗಳ ವಿತರಣೆ
ಸರಪಳಿಯು ಕಿರ್ಚಾಫ್‌ನ ಎರಡನೇ ನಿಯಮವನ್ನು ಪಾಲಿಸುತ್ತದೆ.

ಕಿರ್ಚಾಫ್ ಕಾನೂನುಗಳು
ಓಮ್ನ ನಿಯಮದ ಜೊತೆಗೆ ಮುಖ್ಯ
ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ಗಳ ಸಿದ್ಧಾಂತದಲ್ಲಿ.

ಮೊದಲ
ಕಿರ್ಚಾಫ್ ಕಾನೂನು:

ಬೀಜಗಣಿತ
ನೋಡ್‌ನಲ್ಲಿನ ಪ್ರವಾಹಗಳ ಮೊತ್ತವು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ:

_i
= 0 (19)

ಎಲ್ಲಿ
i
ಕೊಟ್ಟಿರುವ ನೋಡ್‌ನಲ್ಲಿ ಒಮ್ಮುಖವಾಗುವ ಶಾಖೆಗಳ ಸಂಖ್ಯೆ.

ಅಂದರೆ, ಸಂಕಲನ
ಶಾಖೆಗಳಲ್ಲಿನ ಪ್ರವಾಹಗಳಿಗೆ ವಿಸ್ತರಿಸುತ್ತದೆ,
ಪರಿಗಣಿತದಲ್ಲಿ ಒಮ್ಮುಖವಾಗುವುದು
ನೋಡ್.

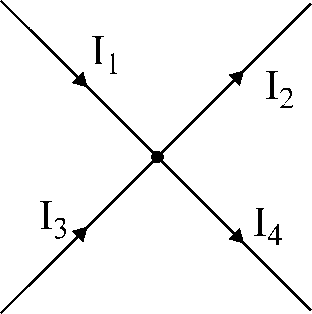
ಚಿತ್ರ.17. ವಿವರಣೆ
ಕಿರ್ಚಾಫ್ನ ಮೊದಲ ನಿಯಮಕ್ಕೆ.

ಸಂಖ್ಯೆ
ಮೊದಲನೆಯ ಪ್ರಕಾರ ಸಮೀಕರಣಗಳನ್ನು ಸಂಕಲಿಸಲಾಗಿದೆ
ಕಿರ್ಚಾಫ್ ನಿಯಮವನ್ನು ಸೂತ್ರದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

ನಪ್
= ನು
– 1,

ಎಲ್ಲಿ
ನು
ಪರಿಗಣಿಸಲಾದ ಸರಪಳಿಯಲ್ಲಿ ನೋಡ್ಗಳ ಸಂಖ್ಯೆ.

ಪ್ರವಾಹಗಳ ಚಿಹ್ನೆಗಳು
ಆಯ್ಕೆಮಾಡಿದದನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು ಸಮೀಕರಣಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ
ಧನಾತ್ಮಕ ನಿರ್ದೇಶನ. ನಲ್ಲಿ ಚಿಹ್ನೆಗಳು
ಪ್ರವಾಹಗಳು ಒಂದೇ ಆಗಿದ್ದರೆ ಪ್ರವಾಹಗಳು ಒಂದೇ ಆಗಿರುತ್ತವೆ
ಇದಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಆಧಾರಿತವಾಗಿದೆ
ನೋಡ್.

ಉದಾಹರಣೆಗೆ,
ಚಿತ್ರ 17 ರಲ್ಲಿ ತೋರಿಸಿರುವ ನೋಡ್‌ಗಾಗಿ:
ನೋಡ್‌ಗೆ ಹರಿಯುವ ಪ್ರವಾಹಗಳಿಗೆ ನಾವು ಚಿಹ್ನೆಗಳನ್ನು ನಿಯೋಜಿಸುತ್ತೇವೆ
"+", ಮತ್ತು ನೋಡ್ನಿಂದ ಹರಿಯುವ ಪ್ರವಾಹಗಳಿಗೆ - ಚಿಹ್ನೆಗಳು
«-».

ನಂತರ ಸಮೀಕರಣ
ಕಿರ್ಚಾಫ್ ಅವರ ಮೊದಲ ಕಾನೂನಿನ ಪ್ರಕಾರ, ಅದನ್ನು ಬರೆಯಲಾಗುತ್ತದೆ
ಆದ್ದರಿಂದ:

I₁
- ಐ₂
+ ಐ₃
- ಐ₄
= 0.

ಸಮೀಕರಣಗಳು,
ಕಿರ್ಚಾಫ್ನ ಮೊದಲ ಕಾನೂನಿನ ಪ್ರಕಾರ ಸಂಕಲಿಸಲಾಗಿದೆ,
ನೋಡ್ಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಈ
ನೋಡ್‌ನಲ್ಲಿರುವ ಅಂಶವನ್ನು ಕಾನೂನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ
ವಿದ್ಯುತ್ ಚಾರ್ಜ್ ಸಂಗ್ರಹವಾಗುವುದಿಲ್ಲ
ಮತ್ತು ಸೇವಿಸಲಾಗುವುದಿಲ್ಲ. ವಿದ್ಯುತ್ ಪ್ರಮಾಣ
ಸೈಟ್‌ಗೆ ಬರುವ ಶುಲ್ಕಗಳು ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ
ನೋಡ್ ಅನ್ನು ಒಂದೇ ಮತ್ತು ಒಂದೇ ಆಗಿ ಬಿಡುವ ಶುಲ್ಕಗಳು
ಅದೇ ಅವಧಿ.

ಎರಡನೇ
ಕಿರ್ಚಾಫ್ ಕಾನೂನು:

ಬೀಜಗಣಿತ
ಇಎಮ್ಎಫ್ ಮೊತ್ತ ಯಾವುದೇ ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ
ಸರಪಳಿಯು ಜಲಪಾತದ ಬೀಜಗಣಿತದ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ
ಈ ಸರ್ಕ್ಯೂಟ್ನ ಅಂಶಗಳ ಮೇಲೆ ವೋಲ್ಟೇಜ್:

Ui
= 
Ei

IiRi=Ei(20)

ಎಲ್ಲಿ
i
- ಅಂಶ ಸಂಖ್ಯೆ (ಪ್ರತಿರೋಧ ಅಥವಾ
ವೋಲ್ಟೇಜ್ ಮೂಲ) ಪರಿಗಣಿಸಲಾಗಿದೆ
ಬಾಹ್ಯರೇಖೆ.

**ಸಂಖ್ಯೆ
ಎರಡನೆಯ ಪ್ರಕಾರ ಸಮೀಕರಣಗಳನ್ನು ಸಂಕಲಿಸಲಾಗಿದೆ
ಕಿರ್ಚಾಫ್ ನಿಯಮವನ್ನು ಸೂತ್ರದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

ನಪ್
= Nb
- ನು
+ 1 - Ned.s.

ಎಲ್ಲಿ
ಎನ್ಬಿ
- ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಶಾಖೆಗಳ ಸಂಖ್ಯೆ;

ನು
- ನೋಡ್ಗಳ ಸಂಖ್ಯೆ;

ನೆಡ್.ಎಸ್.
ಆದರ್ಶ ಇಎಮ್ಎಫ್ ಮೂಲಗಳ ಸಂಖ್ಯೆ.

ಚಿತ್ರ.18. ವಿವರಣೆ
ಕಿರ್ಚಾಫ್ನ ಎರಡನೇ ನಿಯಮಕ್ಕೆ.

ಇದಕ್ಕಾಗಿ,
ಎರಡನೇ ನಿಯಮವನ್ನು ಸರಿಯಾಗಿ ಬರೆಯಲು
ಕೊಟ್ಟಿರುವ ಬಾಹ್ಯರೇಖೆಗಾಗಿ ಕಿರ್ಚಾಫ್, ಅನುಸರಿಸುತ್ತದೆ
ಕೆಳಗಿನ ನಿಯಮಗಳನ್ನು ಅನುಸರಿಸಿ:

1. ನಿರಂಕುಶವಾಗಿ
   ಬಾಹ್ಯರೇಖೆ ಬೈಪಾಸ್‌ನ ದಿಕ್ಕನ್ನು ಆಯ್ಕೆಮಾಡಿ,
   ಉದಾಹರಣೆಗೆ, ಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ (ಚಿತ್ರ 18).

2. emf
   ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ಸ್ ಹೊಂದುತ್ತದೆ
   ಆಯ್ದ ದಿಕ್ಕಿನೊಂದಿಗೆ ದಿಕ್ಕಿನಲ್ಲಿ
   ಬೈಪಾಸ್ ಅನ್ನು ಅಭಿವ್ಯಕ್ತಿಯಲ್ಲಿ ಬರೆಯಲಾಗಿದೆ
   ಚಿಹ್ನೆ "+"; ಒಂದು ವೇಳೆ ಇ.ಎಫ್.ಎಸ್. ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್
   ನಿರ್ದೇಶನಕ್ಕೆ ಹೊಂದಿಕೆಯಾಗುವುದಿಲ್ಲ
   ಬಾಹ್ಯರೇಖೆ, ನಂತರ ಅವುಗಳು ಒಂದು ಚಿಹ್ನೆಯಿಂದ ಮುಂಚಿತವಾಗಿರುತ್ತವೆ
   «-».

ಉದಾಹರಣೆಗೆ,
ಚಿತ್ರ 18 ರ ಬಾಹ್ಯರೇಖೆಗಾಗಿ, ಕಿರ್ಚಾಫ್ನ ಎರಡನೇ ನಿಯಮ
ಈ ಕೆಳಗಿನಂತೆ ಬರೆಯಲಾಗುವುದು:

ಯು₁
- ಯು₂
+ ಯು₃
= ಇ₁
- ಇ₃
- ಇ₄
(21)

ಸಮೀಕರಣ (20) ಆಗಿರಬಹುದು
ಹೀಗೆ ಪುನಃ ಬರೆಯಿರಿ:

 (Ui
-ಇ)
= 0 (22)

ಎಲ್ಲಿ
(ಯು
- ಇ)
- ಶಾಖೆಯ ಮೇಲೆ ಒತ್ತಡ.

ಪರಿಣಾಮವಾಗಿ,
ಕಿರ್ಚಾಫ್ನ ಎರಡನೇ ನಿಯಮವನ್ನು ರೂಪಿಸಬಹುದು
ಕೆಳಗಿನ ರೀತಿಯಲ್ಲಿ:

ಬೀಜಗಣಿತ
ಯಾವುದೇ ಶಾಖೆಗಳ ಮೇಲಿನ ವೋಲ್ಟೇಜ್ಗಳ ಮೊತ್ತ
ಮುಚ್ಚಿದ ಲೂಪ್ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ.

ಸಂಭಾವ್ಯ
ಹಿಂದೆ ಚರ್ಚಿಸಿದ ರೇಖಾಚಿತ್ರವು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ
ಎರಡನೆಯದಕ್ಕೆ ಚಿತ್ರಾತ್ಮಕ ವ್ಯಾಖ್ಯಾನ
ಕಿರ್ಚಾಫ್ ಕಾನೂನು.

ಕಾರ್ಯ ಸಂಖ್ಯೆ 1.

AT
ಚಿತ್ರ 1 ರಲ್ಲಿನ ಸರ್ಕ್ಯೂಟ್ಗೆ ಪ್ರವಾಹಗಳು I ನೀಡಲಾಗಿದೆ₁
ನಾನು ಮತ್ತು₃,
ಪ್ರತಿರೋಧ ಮತ್ತು ಇಎಮ್ಎಫ್ ಪ್ರವಾಹಗಳನ್ನು ನಿರ್ಧರಿಸಿ
I₄,
I₅,
I₆
; ಬಿಂದುಗಳ ನಡುವಿನ ವೋಲ್ಟೇಜ್ a
ಮತ್ತು ಬಿ
ಒಂದು ವೇಳೆ ನಾನು₁
= 10mA,
I₃
= -20 mA,
ಆರ್₄
= 5kOhm,
ಇ₅
= 20B,
ಆರ್₅
= 3kOhm,
ಇ₆
= 40B,
ಆರ್₆
= 2kOhm.

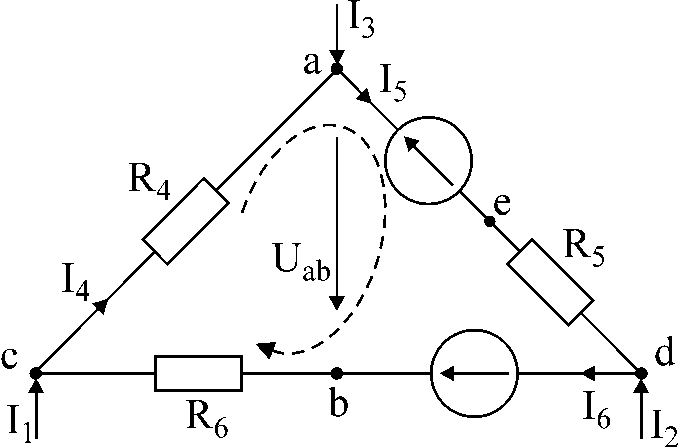
ಚಿತ್ರ.1

ಪರಿಹಾರ:

1. ಕೊಟ್ಟಿದ್ದಕ್ಕಾಗಿ
   ಬಾಹ್ಯರೇಖೆಯ ಪ್ರಕಾರ ನಾವು ಎರಡು ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸುತ್ತೇವೆ
   ಕಿರ್ಚಾಫ್ನ ಮೊದಲ ಕಾನೂನು ಮತ್ತು ಒಂದು - ಪ್ರಕಾರ
   ಎರಡನೇ. ಬಾಹ್ಯರೇಖೆಯ ನಿರ್ದೇಶನ
   ಬಾಣದಿಂದ ಸೂಚಿಸಲಾಗಿದೆ.

AT
ನಾವು ಪಡೆಯುವ ಪರಿಹಾರದ ಪರಿಣಾಮವಾಗಿ: I₆
= 0; I₄
= 10mA;
I₅
= -10mA

1. ಕೇಳು
   ಬಿಂದುಗಳ ನಡುವಿನ ವೋಲ್ಟೇಜ್ ದಿಕ್ಕು
   ಎ
   ಮತ್ತು ಬಿ
   "ಎ" ಬಿಂದುವಿನಿಂದ
   "ಬಿ" ಅನ್ನು ಸೂಚಿಸಲು
   - ಯು_ab.
   ಈ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಸಮೀಕರಣದಿಂದ ಕಂಡುಹಿಡಿಯಬಹುದು
   ಕಿರ್ಚಾಫ್ ಎರಡನೇ ನಿಯಮ:

I₄ಆರ್₄
+ ಯು_ab
+ ಐ₆ಆರ್₆
= 0

ಯು_ab
= - 50 ವಿ.

ಕಾರ್ಯ ಸಂಖ್ಯೆ 2.

ಫಾರ್
ಚಿತ್ರ 2 ರಲ್ಲಿನ ರೇಖಾಚಿತ್ರಗಳು ಪ್ರಕಾರ ಸಮೀಕರಣಗಳನ್ನು ರೂಪಿಸುತ್ತವೆ
ಕಿರ್ಚಾಫ್ ಕಾನೂನುಗಳು ಮತ್ತು ಅಪರಿಚಿತರನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ
ಅಂಕಗಳು.

ನೀಡಿದ:
I₁
= 20mA;
I₂
= 10mA

ಆರ್₁
= 5kOhm,
ಆರ್₃
= 4kOhm,
ಆರ್₄
= 6kOhm,
ಆರ್₅
= 2kOhm,
ಆರ್₆
= 4kΩ.

Fig.2

ಪರಿಹಾರ:

ನೋಡ್ಗಳ ಸಂಖ್ಯೆ
ಸಮೀಕರಣಗಳು - 3, ಬಾಹ್ಯರೇಖೆ ಸಮೀಕರಣಗಳ ಸಂಖ್ಯೆ
– 1.

ನೆನಪಿಡಿ!
ಎರಡನೆಯ ಪ್ರಕಾರ ಸಮೀಕರಣವನ್ನು ಕಂಪೈಲ್ ಮಾಡುವಾಗ
ಕಿರ್ಚಾಫ್ ಕಾನೂನು, ನಾವು ಬಾಹ್ಯರೇಖೆಯನ್ನು ಆಯ್ಕೆ ಮಾಡುತ್ತೇವೆ
ಪ್ರಸ್ತುತ ಮೂಲಗಳನ್ನು ಒಳಗೊಂಡಿಲ್ಲ.
ಬಾಹ್ಯರೇಖೆಯ ದಿಕ್ಕನ್ನು ಚಿತ್ರದಲ್ಲಿ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

AT
ಈ ಸರ್ಕ್ಯೂಟ್ನ, ಶಾಖೆಗಳ ಪ್ರವಾಹಗಳು I₁
ನಾನು ಮತ್ತು₂.
ಅಜ್ಞಾತ
ಪ್ರವಾಹಗಳು
I₃,
I₄,
I₅,
I₆.

ನಿರ್ಧರಿಸುವುದು
ವ್ಯವಸ್ಥೆ, ನಾವು ಪಡೆಯುತ್ತೇವೆ: I₃
= 13.75 mA;
I₄
= -3.75mA;
I₅
= 6.25mA;
I₆
= 16.25mA.

ಮೂಲ ಪರಿಕಲ್ಪನೆಗಳು

ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಹೆಚ್ಚಿನ ಸಾಮರ್ಥ್ಯದಿಂದ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಕಡಿಮೆ ಒಂದಕ್ಕೆ ಚಲಿಸಲು ಅನುಮತಿಸಿದಾಗ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಹರಿಯುತ್ತದೆ. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಪ್ರವಾಹಕ್ಕೆ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಮೂಲ ಅಗತ್ಯವಿರುತ್ತದೆ, ಅದು ಅವುಗಳನ್ನು ಚಲನೆಯಲ್ಲಿ ಹೊಂದಿಸಲು ಶಕ್ತಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಜೊತೆಗೆ ಅವುಗಳ ಕೊರತೆಯಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟ ಋಣಾತ್ಮಕ ಶುಲ್ಕಗಳ ಹಿಂತಿರುಗಿಸುವ ಬಿಂದುವಾಗಿದೆ. ಭೌತಿಕ ವಿದ್ಯಮಾನವಾಗಿ, ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ಪ್ರವಾಹವು ಮೂರು ಮೂಲಭೂತ ಪ್ರಮಾಣಗಳಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟಿದೆ:

• ವೋಲ್ಟೇಜ್;
• ಪ್ರಸ್ತುತ ಶಕ್ತಿ;
• ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಚಲಿಸುವ ವಾಹಕದ ಪ್ರತಿರೋಧ.

ಶಕ್ತಿ ಮತ್ತು ಒತ್ತಡ

ಪ್ರಸ್ತುತ ಶಕ್ತಿ (I, ಆಂಪಿಯರ್‌ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ) ಎಂಬುದು ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಪರಿಮಾಣವಾಗಿದೆ (ಚಾರ್ಜ್) ಪ್ರತಿ ಯುನಿಟ್ ಸಮಯದ ಪ್ರತಿ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಸ್ಥಳದ ಮೂಲಕ ಚಲಿಸುತ್ತದೆ.ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಮಾಪನ I ಎಂಬುದು ಚಲನೆಯಲ್ಲಿರುವ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಸಂಖ್ಯೆಯ ನಿರ್ಣಯವಾಗಿದೆ

ಪದವು ಚಲನೆಯನ್ನು ಮಾತ್ರ ಸೂಚಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಬಹಳ ಮುಖ್ಯ: ಸ್ಥಿರ ಶುಲ್ಕಗಳು, ಉದಾಹರಣೆಗೆ, ಸಂಪರ್ಕವಿಲ್ಲದ ಬ್ಯಾಟರಿಯ ಟರ್ಮಿನಲ್‌ಗಳಲ್ಲಿ, I ನ ಅಳೆಯಬಹುದಾದ ಮೌಲ್ಯವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ. ಒಂದು ದಿಕ್ಕಿನಲ್ಲಿ ಹರಿಯುವ ಪ್ರವಾಹವನ್ನು ನೇರ (DC) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು ನಿಯತಕಾಲಿಕವಾಗಿ ಬದಲಾಗುತ್ತಿರುವ ದಿಕ್ಕನ್ನು ಪರ್ಯಾಯ (AC) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಒತ್ತಡದಂತಹ ವಿದ್ಯಮಾನದಿಂದ ಅಥವಾ ಗುರುತ್ವಾಕರ್ಷಣೆಯ ಪ್ರಭಾವದ ಅಡಿಯಲ್ಲಿ ವಸ್ತುಗಳ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯಲ್ಲಿನ ವ್ಯತ್ಯಾಸದಿಂದ ವೋಲ್ಟೇಜ್ ಅನ್ನು ವಿವರಿಸಬಹುದು.

ಈ ಅಸಮತೋಲನವನ್ನು ಸೃಷ್ಟಿಸಲು, ನೀವು ಮೊದಲು ಶಕ್ತಿಯನ್ನು ವ್ಯಯಿಸಬೇಕು, ಇದು ಸೂಕ್ತವಾದ ಸಂದರ್ಭಗಳಲ್ಲಿ ಚಲನೆಯಲ್ಲಿ ಅರಿತುಕೊಳ್ಳುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಎತ್ತರದಿಂದ ಹೊರೆ ಬಿದ್ದಾಗ, ಅದನ್ನು ಎತ್ತುವ ಕೆಲಸವನ್ನು ಕೈಗೊಳ್ಳಲಾಗುತ್ತದೆ, ಗ್ಯಾಲ್ವನಿಕ್ ಬ್ಯಾಟರಿಗಳಲ್ಲಿ, ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಪರಿವರ್ತನೆಯಿಂದಾಗಿ ಟರ್ಮಿನಲ್‌ಗಳಲ್ಲಿ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು ರೂಪುಗೊಳ್ಳುತ್ತದೆ, ಜನರೇಟರ್‌ಗಳಲ್ಲಿ - ಒಡ್ಡುವಿಕೆಯ ಪರಿಣಾಮವಾಗಿ ಒಂದು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರ

ಒತ್ತಡದಂತಹ ವಿದ್ಯಮಾನದಿಂದ ಅಥವಾ ಗುರುತ್ವಾಕರ್ಷಣೆಯ ಪ್ರಭಾವದ ಅಡಿಯಲ್ಲಿ ವಸ್ತುಗಳ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯ ವ್ಯತ್ಯಾಸದಿಂದ ಒತ್ತಡವನ್ನು ವಿವರಿಸಬಹುದು. ಈ ಅಸಮತೋಲನವನ್ನು ಸೃಷ್ಟಿಸಲು, ನೀವು ಮೊದಲು ಶಕ್ತಿಯನ್ನು ವ್ಯಯಿಸಬೇಕು, ಇದು ಸೂಕ್ತವಾದ ಸಂದರ್ಭಗಳಲ್ಲಿ ಚಲನೆಯಲ್ಲಿ ಅರಿತುಕೊಳ್ಳುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಎತ್ತರದಿಂದ ಹೊರೆ ಬೀಳುವಾಗ, ಅದನ್ನು ಎತ್ತುವ ಕೆಲಸವನ್ನು ಅರಿತುಕೊಳ್ಳಲಾಗುತ್ತದೆ, ಗ್ಯಾಲ್ವನಿಕ್ ಬ್ಯಾಟರಿಗಳಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಪರಿವರ್ತನೆಯಿಂದಾಗಿ ಟರ್ಮಿನಲ್‌ಗಳಲ್ಲಿ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು ರೂಪುಗೊಳ್ಳುತ್ತದೆ, ಜನರೇಟರ್‌ಗಳಲ್ಲಿ - ಒಡ್ಡಿಕೆಯ ಪರಿಣಾಮವಾಗಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರ.

ಕಂಡಕ್ಟರ್ ಪ್ರತಿರೋಧ

ಸಾಮಾನ್ಯ ಕಂಡಕ್ಟರ್ ಎಷ್ಟೇ ಉತ್ತಮವಾಗಿದ್ದರೂ, ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಅವುಗಳ ಚಲನೆಗೆ ಸ್ವಲ್ಪ ಪ್ರತಿರೋಧವಿಲ್ಲದೆ ಹಾದುಹೋಗಲು ಎಂದಿಗೂ ಅನುಮತಿಸುವುದಿಲ್ಲ.ಯಾಂತ್ರಿಕ ಘರ್ಷಣೆಯ ಅನಾಲಾಗ್ ಆಗಿ ಪ್ರತಿರೋಧವನ್ನು ಪರಿಗಣಿಸಲು ಸಾಧ್ಯವಿದೆ, ಆದಾಗ್ಯೂ ಈ ಹೋಲಿಕೆ ಪರಿಪೂರ್ಣವಾಗುವುದಿಲ್ಲ. ವಾಹಕದ ಮೂಲಕ ಪ್ರಸ್ತುತ ಹರಿಯುವಾಗ, ಕೆಲವು ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವನ್ನು ಶಾಖವಾಗಿ ಪರಿವರ್ತಿಸಲಾಗುತ್ತದೆ, ಆದ್ದರಿಂದ ಯಾವಾಗಲೂ ಪ್ರತಿರೋಧಕದ ಮೇಲೆ ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ ಇರುತ್ತದೆ. ಎಲೆಕ್ಟ್ರಿಕ್ ಹೀಟರ್‌ಗಳು, ಹೇರ್ ಡ್ರೈಯರ್‌ಗಳು ಮತ್ತು ಇತರ ರೀತಿಯ ಸಾಧನಗಳನ್ನು ಶಾಖದ ರೂಪದಲ್ಲಿ ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಹೊರಹಾಕಲು ಮಾತ್ರ ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ.

ಸರಳೀಕೃತ ಪ್ರತಿರೋಧ (ಆರ್ ಎಂದು ಸೂಚಿಸಲಾಗುತ್ತದೆ) ಒಂದು ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಹರಿವು ಎಷ್ಟು ಹಿಂದುಳಿದಿದೆ ಎಂಬುದರ ಅಳತೆಯಾಗಿದೆ. ಇದನ್ನು ಓಮ್ನಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ. ಪ್ರತಿರೋಧಕ ಅಥವಾ ಇತರ ಅಂಶದ ವಾಹಕತೆಯನ್ನು ಎರಡು ಗುಣಲಕ್ಷಣಗಳಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

• ರೇಖಾಗಣಿತ;
• ವಸ್ತು.

ಹೈಡ್ರಾಲಿಕ್ ಸಾದೃಶ್ಯದಿಂದ ಸ್ಪಷ್ಟವಾದಂತೆ ಆಕಾರವು ಅತ್ಯಂತ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಹೊಂದಿದೆ: ಉದ್ದ ಮತ್ತು ಕಿರಿದಾದ ಪೈಪ್ ಮೂಲಕ ನೀರನ್ನು ತಳ್ಳುವುದು ಚಿಕ್ಕ ಮತ್ತು ಅಗಲದ ಮೂಲಕ ನೀರನ್ನು ತಳ್ಳುವುದಕ್ಕಿಂತ ಹೆಚ್ಚು ಕಷ್ಟ. ವಸ್ತುಗಳು ನಿರ್ಣಾಯಕ ಪಾತ್ರವನ್ನು ವಹಿಸುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ತಾಮ್ರದ ತಂತಿಯಲ್ಲಿ ಮುಕ್ತವಾಗಿ ಚಲಿಸಬಹುದು, ಆದರೆ ಅವುಗಳ ಆಕಾರವನ್ನು ಲೆಕ್ಕಿಸದೆ ರಬ್ಬರ್‌ನಂತಹ ಅವಾಹಕಗಳ ಮೂಲಕ ಹರಿಯುವುದಿಲ್ಲ. ಜ್ಯಾಮಿತಿ ಮತ್ತು ವಸ್ತುಗಳ ಜೊತೆಗೆ, ವಾಹಕತೆಯ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುವ ಇತರ ಅಂಶಗಳಿವೆ.

ಓಮ್ನ ಕಾನೂನಿನ ವ್ಯಾಖ್ಯಾನ

ಆರೋಪಗಳ ಚಲನೆಯನ್ನು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಲು, ನೀವು ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಮುಚ್ಚಬೇಕಾಗುತ್ತದೆ. ಹೆಚ್ಚುವರಿ ಶಕ್ತಿಯ ಅನುಪಸ್ಥಿತಿಯಲ್ಲಿ, ಪ್ರಸ್ತುತವು ದೀರ್ಘಕಾಲದವರೆಗೆ ಅಸ್ತಿತ್ವದಲ್ಲಿರಲು ಸಾಧ್ಯವಿಲ್ಲ. ಸಂಭಾವ್ಯತೆಯು ತ್ವರಿತವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಸರ್ಕ್ಯೂಟ್ನ ಆಪರೇಟಿಂಗ್ ಮೋಡ್ ಅನ್ನು ನಿರ್ವಹಿಸಲು, ಹೆಚ್ಚುವರಿ ಮೂಲ (ಜನರೇಟರ್, ಬ್ಯಾಟರಿ) ಅಗತ್ಯವಿದೆ.

ಸಂಪೂರ್ಣ ಸರ್ಕ್ಯೂಟ್ ಎಲ್ಲಾ ಘಟಕಗಳ ಒಟ್ಟು ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ನಿಖರವಾದ ಲೆಕ್ಕಾಚಾರಗಳಿಗಾಗಿ, ವಾಹಕಗಳಲ್ಲಿನ ನಷ್ಟಗಳು, ಪ್ರತಿರೋಧಕ ಅಂಶಗಳು ಮತ್ತು ವಿದ್ಯುತ್ ಮೂಲವನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ.

ನಿರ್ದಿಷ್ಟ ವಿದ್ಯುತ್ ಬಲಕ್ಕೆ ಎಷ್ಟು ವೋಲ್ಟೇಜ್ ಅನ್ನು ಅನ್ವಯಿಸಬೇಕು ಎಂಬುದನ್ನು ಸೂತ್ರದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ:

U=I*R.

ಅಂತೆಯೇ, ಪರಿಗಣಿಸಲಾದ ಸಂಬಂಧಗಳ ಸಹಾಯದಿಂದ, ಸರ್ಕ್ಯೂಟ್ನ ಇತರ ನಿಯತಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ಸಮಾನಾಂತರ ಮತ್ತು ಸರಣಿ ಸಂಪರ್ಕ

ಎಲೆಕ್ಟ್ರಿಕ್ಸ್‌ನಲ್ಲಿ, ಅಂಶಗಳನ್ನು ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಲಾಗಿದೆ - ಒಂದರ ನಂತರ ಒಂದರಂತೆ ಅಥವಾ ಸಮಾನಾಂತರವಾಗಿ - ಹಲವಾರು ಇನ್‌ಪುಟ್‌ಗಳನ್ನು ಒಂದು ಬಿಂದುಕ್ಕೆ ಸಂಪರ್ಕಿಸಿದಾಗ ಮತ್ತು ಅದೇ ಅಂಶಗಳ ಔಟ್‌ಪುಟ್‌ಗಳು ಇನ್ನೊಂದಕ್ಕೆ ಸಂಪರ್ಕಗೊಂಡಾಗ.

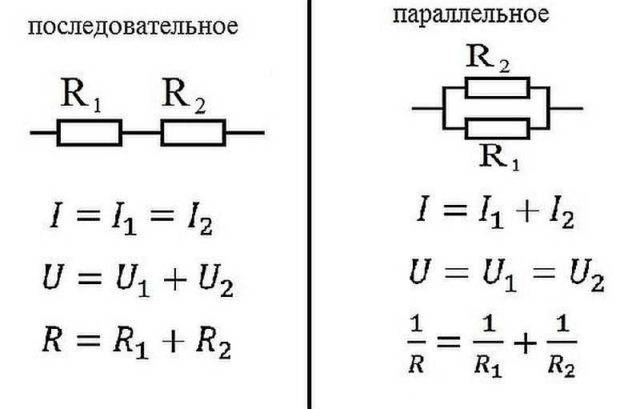
ಸಮಾನಾಂತರ ಮತ್ತು ಸರಣಿ ಸಂಪರ್ಕಕ್ಕಾಗಿ ಓಮ್ನ ನಿಯಮ

ಸರಣಿ ಸಂಪರ್ಕ

ಈ ಪ್ರಕರಣಗಳಿಗೆ ಓಮ್‌ನ ಕಾನೂನು ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ? ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಿದಾಗ, ಅಂಶಗಳ ಸರಪಳಿಯ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹವು ಒಂದೇ ಆಗಿರುತ್ತದೆ. ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಲಾದ ಅಂಶಗಳೊಂದಿಗೆ ಸರ್ಕ್ಯೂಟ್ನ ವಿಭಾಗದ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಪ್ರತಿ ವಿಭಾಗದಲ್ಲಿನ ವೋಲ್ಟೇಜ್ಗಳ ಮೊತ್ತವಾಗಿ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ಇದನ್ನು ಹೇಗೆ ವಿವರಿಸಬಹುದು? ಒಂದು ಅಂಶದ ಮೂಲಕ ಪ್ರವಾಹದ ಹರಿವು ಚಾರ್ಜ್ನ ಭಾಗವನ್ನು ಅದರ ಒಂದು ಭಾಗದಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ವರ್ಗಾಯಿಸುವುದು. ನನ್ನ ಪ್ರಕಾರ, ಇದು ಸ್ವಲ್ಪ ಕೆಲಸ. ಈ ಕೆಲಸದ ಪ್ರಮಾಣವು ಒತ್ತಡವಾಗಿದೆ. ಇದು ಒತ್ತಡದ ಭೌತಿಕ ಅರ್ಥವಾಗಿದೆ. ಇದು ಸ್ಪಷ್ಟವಾಗಿದ್ದರೆ, ನಾವು ಮುಂದುವರಿಯುತ್ತೇವೆ.

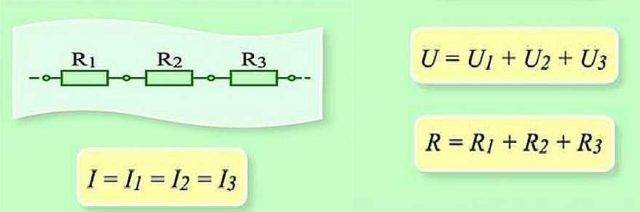
ಸರ್ಕ್ಯೂಟ್ನ ಈ ವಿಭಾಗದ ಸರಣಿ ಸಂಪರ್ಕ ಮತ್ತು ನಿಯತಾಂಕಗಳು

ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಿದಾಗ, ಪ್ರತಿ ಅಂಶದ ಮೂಲಕ ಪ್ರತಿಯಾಗಿ ಚಾರ್ಜ್ ಅನ್ನು ವರ್ಗಾಯಿಸುವುದು ಅವಶ್ಯಕ. ಮತ್ತು ಪ್ರತಿ ಅಂಶದ ಮೇಲೆ, ಇದು ಕೆಲಸದ ಒಂದು ನಿರ್ದಿಷ್ಟ "ಪರಿಮಾಣ" ಆಗಿದೆ. ಮತ್ತು ಸರಪಳಿಯ ಸಂಪೂರ್ಣ ವಿಭಾಗದಲ್ಲಿ ಕೆಲಸದ ಪ್ರಮಾಣವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನೀವು ಪ್ರತಿ ಅಂಶದ ಮೇಲೆ ಕೆಲಸವನ್ನು ಸೇರಿಸಬೇಕಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ ಒಟ್ಟು ವೋಲ್ಟೇಜ್ ಪ್ರತಿಯೊಂದು ಅಂಶಗಳ ಮೇಲಿನ ವೋಲ್ಟೇಜ್ಗಳ ಮೊತ್ತವಾಗಿದೆ ಎಂದು ಅದು ತಿರುಗುತ್ತದೆ.

ಅದೇ ರೀತಿಯಲ್ಲಿ - ಸೇರ್ಪಡೆಯ ಸಹಾಯದಿಂದ - ಸರ್ಕ್ಯೂಟ್ ವಿಭಾಗದ ಒಟ್ಟು ಪ್ರತಿರೋಧವೂ ಕಂಡುಬರುತ್ತದೆ. ನೀವು ಅದನ್ನು ಹೇಗೆ ಊಹಿಸಬಹುದು? ಅಂಶಗಳ ಸರಪಳಿಯ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹವು ಅನುಕ್ರಮವಾಗಿ ಎಲ್ಲಾ ಪ್ರತಿರೋಧಗಳನ್ನು ಮೀರಿಸುತ್ತದೆ. ಒಂದೊಂದಾಗಿ. ಅಂದರೆ, ಅವನು ಜಯಿಸಿದ ಪ್ರತಿರೋಧವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಪ್ರತಿರೋಧಗಳನ್ನು ಸೇರಿಸುವುದು ಅವಶ್ಯಕ. ಹೆಚ್ಚು ಕಡಿಮೆ ಹೀಗೆ.ಗಣಿತದ ವ್ಯುತ್ಪನ್ನವು ಹೆಚ್ಚು ಜಟಿಲವಾಗಿದೆ ಮತ್ತು ಈ ಕಾನೂನಿನ ಕಾರ್ಯವಿಧಾನವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಸುಲಭವಾಗಿದೆ.

ಸಮಾನಾಂತರ ಸಂಪರ್ಕ

ವಾಹಕಗಳು / ಅಂಶಗಳ ಪ್ರಾರಂಭಗಳು ಒಂದು ಹಂತದಲ್ಲಿ ಒಮ್ಮುಖವಾಗುವುದು ಮತ್ತು ಇನ್ನೊಂದರಲ್ಲಿ ಅವುಗಳ ತುದಿಗಳು ಸಂಪರ್ಕಗೊಂಡಾಗ ಸಮಾನಾಂತರ ಸಂಪರ್ಕವಾಗಿದೆ. ಈ ಪ್ರಕಾರದ ಸಂಯುಕ್ತಗಳಿಗೆ ಮಾನ್ಯವಾಗಿರುವ ಕಾನೂನುಗಳನ್ನು ವಿವರಿಸಲು ನಾವು ಪ್ರಯತ್ನಿಸುತ್ತೇವೆ. ಕರೆಂಟ್‌ನಿಂದ ಪ್ರಾರಂಭಿಸೋಣ. ಅಂಶಗಳ ಸಂಪರ್ಕ ಬಿಂದುವಿಗೆ ಕೆಲವು ಪ್ರಮಾಣದ ಪ್ರವಾಹವನ್ನು ಸರಬರಾಜು ಮಾಡಲಾಗುತ್ತದೆ. ಇದು ಪ್ರತ್ಯೇಕಿಸುತ್ತದೆ, ಎಲ್ಲಾ ವಾಹಕಗಳ ಮೂಲಕ ಹರಿಯುತ್ತದೆ. ಇದರಿಂದ ನಾವು ವಿಭಾಗದಲ್ಲಿನ ಒಟ್ಟು ಪ್ರವಾಹವು ಪ್ರತಿಯೊಂದು ಅಂಶಗಳಲ್ಲಿನ ಪ್ರವಾಹದ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಎಂದು ನಾವು ತೀರ್ಮಾನಿಸುತ್ತೇವೆ: I = I1 + I2 + I3.

ಈಗ ವೋಲ್ಟೇಜ್ಗಾಗಿ. ಚಾರ್ಜ್ ಅನ್ನು ಸರಿಸಲು ವೋಲ್ಟೇಜ್ ಕೆಲಸವಾಗಿದ್ದರೆ, ಒಂದು ಚಾರ್ಜ್ ಅನ್ನು ಸರಿಸಲು ಅಗತ್ಯವಿರುವ ಕೆಲಸವು ಯಾವುದೇ ಅಂಶದ ಮೇಲೆ ಒಂದೇ ಆಗಿರುತ್ತದೆ. ಅಂದರೆ, ಪ್ರತಿ ಸಮಾನಾಂತರ ಸಂಪರ್ಕಿತ ಅಂಶದಲ್ಲಿನ ವೋಲ್ಟೇಜ್ ಒಂದೇ ಆಗಿರುತ್ತದೆ. U=U1=U2=U3. ಸರಪಳಿ ವಿಭಾಗಕ್ಕೆ ಓಮ್ನ ಕಾನೂನಿನ ವಿವರಣೆಯ ಸಂದರ್ಭದಲ್ಲಿ ವಿನೋದ ಮತ್ತು ದೃಶ್ಯವಲ್ಲ, ಆದರೆ ನೀವು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬಹುದು.

ಸಮಾನಾಂತರ ಸಂಪರ್ಕಕ್ಕಾಗಿ ಕಾನೂನುಗಳು

ಪ್ರತಿರೋಧಕ್ಕಾಗಿ, ವಿಷಯಗಳು ಸ್ವಲ್ಪ ಹೆಚ್ಚು ಜಟಿಲವಾಗಿವೆ. ವಾಹಕತೆಯ ಪರಿಕಲ್ಪನೆಯನ್ನು ಪರಿಚಯಿಸೋಣ. ಈ ವಾಹಕದ ಮೂಲಕ ಚಾರ್ಜ್ ಹಾದುಹೋಗಲು ಎಷ್ಟು ಸುಲಭ ಅಥವಾ ಕಷ್ಟ ಎಂದು ಸೂಚಿಸುವ ವಿಶಿಷ್ಟ ಲಕ್ಷಣವಾಗಿದೆ. ಕಡಿಮೆ ಪ್ರತಿರೋಧ, ಪ್ರಸ್ತುತ ಹಾದುಹೋಗಲು ಸುಲಭವಾಗುತ್ತದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಆದ್ದರಿಂದ, ವಾಹಕತೆ - ಜಿ - ಪ್ರತಿರೋಧದ ಪರಸ್ಪರ ಎಂದು ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ಸೂತ್ರದಲ್ಲಿ, ಇದು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ: G = 1/R.

ನಾವು ವಾಹಕತೆಯ ಬಗ್ಗೆ ಏಕೆ ಮಾತನಾಡುತ್ತಿದ್ದೇವೆ? ಏಕೆಂದರೆ ಅಂಶಗಳ ಸಮಾನಾಂತರ ಸಂಪರ್ಕವನ್ನು ಹೊಂದಿರುವ ವಿಭಾಗದ ಒಟ್ಟು ವಾಹಕತೆಯು ಪ್ರತಿಯೊಂದು ವಿಭಾಗಗಳ ವಾಹಕತೆಯ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. G = G1 + G2 + G3 - ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಸುಲಭ. ಸಮಾನಾಂತರ ಅಂಶಗಳ ಈ ನೋಡ್ ಅನ್ನು ಪ್ರವಾಹವು ಎಷ್ಟು ಸುಲಭವಾಗಿ ಜಯಿಸುತ್ತದೆ ಎಂಬುದು ಪ್ರತಿಯೊಂದು ಅಂಶಗಳ ವಾಹಕತೆಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಆದ್ದರಿಂದ ಅವರು ಮಡಚಬೇಕಾಗಿದೆ ಎಂದು ಅದು ತಿರುಗುತ್ತದೆ.

ಈಗ ನಾವು ಪ್ರತಿರೋಧಕ್ಕೆ ಹೋಗಬಹುದು.ವಾಹಕತೆಯು ಪ್ರತಿರೋಧದ ಪರಸ್ಪರ ಸಂಬಂಧವಾಗಿರುವುದರಿಂದ, ನಾವು ಈ ಕೆಳಗಿನ ಸೂತ್ರವನ್ನು ಪಡೆಯಬಹುದು: 1/R = 1/R1 + 1/R2 + 1/R3.

ನಮಗೆ ಸಮಾನಾಂತರ ಮತ್ತು ಸರಣಿ ಸಂಪರ್ಕವನ್ನು ಯಾವುದು ನೀಡುತ್ತದೆ?

ಸೈದ್ಧಾಂತಿಕ ಜ್ಞಾನವು ಒಳ್ಳೆಯದು, ಆದರೆ ಅದನ್ನು ಆಚರಣೆಯಲ್ಲಿ ಹೇಗೆ ಅನ್ವಯಿಸಬೇಕು? ಯಾವುದೇ ರೀತಿಯ ಅಂಶಗಳನ್ನು ಸಮಾನಾಂತರವಾಗಿ ಮತ್ತು ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಬಹುದು. ಆದರೆ ರೇಖೀಯ ಅಂಶಗಳನ್ನು ವಿವರಿಸುವ ಸರಳ ಸೂತ್ರಗಳನ್ನು ಮಾತ್ರ ನಾವು ಪರಿಗಣಿಸಿದ್ದೇವೆ. ರೇಖೀಯ ಅಂಶಗಳು ಪ್ರತಿರೋಧಗಳಾಗಿವೆ, ಇದನ್ನು "ರೆಸಿಸ್ಟರ್ಗಳು" ಎಂದೂ ಕರೆಯುತ್ತಾರೆ. ಆದ್ದರಿಂದ ನೀವು ಕಲಿತದ್ದನ್ನು ನೀವು ಹೇಗೆ ಬಳಸಬಹುದು ಎಂಬುದು ಇಲ್ಲಿದೆ:

ಯಾವುದೇ ದೊಡ್ಡ-ಮೌಲ್ಯದ ರೆಸಿಸ್ಟರ್ ಲಭ್ಯವಿಲ್ಲದಿದ್ದರೆ, ಆದರೆ ಹಲವಾರು ಚಿಕ್ಕವುಗಳಿದ್ದರೆ, ಸರಣಿಯಲ್ಲಿ ಹಲವಾರು ಪ್ರತಿರೋಧಕಗಳನ್ನು ಸಂಪರ್ಕಿಸುವ ಮೂಲಕ ಅಪೇಕ್ಷಿತ ಪ್ರತಿರೋಧವನ್ನು ಪಡೆಯಬಹುದು. ನೀವು ನೋಡುವಂತೆ, ಇದು ಉಪಯುಕ್ತ ಟ್ರಿಕ್ ಆಗಿದೆ.
ಬ್ಯಾಟರಿಗಳ ಜೀವನವನ್ನು ವಿಸ್ತರಿಸಲು, ಅವುಗಳನ್ನು ಸಮಾನಾಂತರವಾಗಿ ಸಂಪರ್ಕಿಸಬಹುದು. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಓಮ್ನ ಕಾನೂನಿನ ಪ್ರಕಾರ ವೋಲ್ಟೇಜ್ ಒಂದೇ ಆಗಿರುತ್ತದೆ (ಮಲ್ಟಿಮೀಟರ್ನೊಂದಿಗೆ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಅಳೆಯುವ ಮೂಲಕ ನೀವು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಬಹುದು). ಮತ್ತು ಡ್ಯುಯಲ್ ಬ್ಯಾಟರಿಯ "ಜೀವಮಾನ" ಪರಸ್ಪರ ಬದಲಿಸುವ ಎರಡು ಅಂಶಗಳಿಗಿಂತ ಹೆಚ್ಚು ಉದ್ದವಾಗಿರುತ್ತದೆ

ಕೇವಲ ಗಮನಿಸಿ: ಒಂದೇ ಸಾಮರ್ಥ್ಯದೊಂದಿಗೆ ವಿದ್ಯುತ್ ಸರಬರಾಜುಗಳನ್ನು ಮಾತ್ರ ಸಮಾನಾಂತರವಾಗಿ ಸಂಪರ್ಕಿಸಬಹುದು. ಅಂದರೆ, ಸತ್ತ ಮತ್ತು ಹೊಸ ಬ್ಯಾಟರಿಯನ್ನು ಸಂಪರ್ಕಿಸಲಾಗುವುದಿಲ್ಲ.

ನೀವು ಇನ್ನೂ ಸಂಪರ್ಕಿಸಿದರೆ, ದೊಡ್ಡ ಚಾರ್ಜ್ ಹೊಂದಿರುವ ಬ್ಯಾಟರಿಯು ಕಡಿಮೆ ಚಾರ್ಜ್ ಮಾಡಲಾದ ಒಂದನ್ನು ಚಾರ್ಜ್ ಮಾಡುತ್ತದೆ. ಪರಿಣಾಮವಾಗಿ, ಅವರ ಒಟ್ಟು ಚಾರ್ಜ್ ಕಡಿಮೆ ಮೌಲ್ಯಕ್ಕೆ ಇಳಿಯುತ್ತದೆ.

ಸಾಮಾನ್ಯವಾಗಿ, ಈ ಸಂಯುಕ್ತಗಳಿಗೆ ಇವು ಅತ್ಯಂತ ಸಾಮಾನ್ಯವಾದ ಉಪಯೋಗಗಳಾಗಿವೆ.

ಆದರ್ಶ EMF ಮೂಲ

ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ (ಇ) ಎನ್ನುವುದು ಭೌತಿಕ ಪ್ರಮಾಣವಾಗಿದ್ದು, ಚಾರ್ಜ್ ಕ್ಯಾರಿಯರ್‌ಗಳ ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಚಲನೆಯ ಮೇಲೆ ಬಾಹ್ಯ ಶಕ್ತಿಗಳ ಪ್ರಭಾವದ ಮಟ್ಟವನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ವಾಹಕದ ಮೂಲಕ ಪ್ರವಾಹವು ಎಷ್ಟು ಬಲವಾಗಿ ಹರಿಯುತ್ತದೆ ಎಂಬುದು EMF ಅನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.

ಅಂತಹ ಗ್ರಹಿಸಲಾಗದ ವಿದ್ಯಮಾನಗಳನ್ನು ವಿವರಿಸುವಾಗ, ದೇಶೀಯ ಶಾಲಾ ಶಿಕ್ಷಕರು ಹೈಡ್ರಾಲಿಕ್ ಸಾದೃಶ್ಯಗಳ ವಿಧಾನಕ್ಕೆ ತಿರುಗಲು ಇಷ್ಟಪಡುತ್ತಾರೆ. ಕಂಡಕ್ಟರ್ ಒಂದು ಪೈಪ್ ಆಗಿದ್ದರೆ ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಅದರ ಮೂಲಕ ಹರಿಯುವ ನೀರಿನ ಪ್ರಮಾಣವಾಗಿದ್ದರೆ, ಇಎಮ್ಎಫ್ ಎಂಬುದು ಪಂಪ್ ದ್ರವವನ್ನು ಪಂಪ್ ಮಾಡಲು ಅಭಿವೃದ್ಧಿಪಡಿಸುವ ಒತ್ತಡವಾಗಿದೆ.

ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಎಂಬ ಪದವು ವೋಲ್ಟೇಜ್ನಂತಹ ಪರಿಕಲ್ಪನೆಗೆ ಸಂಬಂಧಿಸಿದೆ. ಅವಳು, ಇಎಮ್ಎಫ್, ವೋಲ್ಟ್ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ (ಘಟಕ - "ವಿ"). ಪ್ರತಿಯೊಂದು ವಿದ್ಯುತ್ ಮೂಲವೂ, ಅದು ಬ್ಯಾಟರಿಯಾಗಿರಲಿ, ಜನರೇಟರ್ ಆಗಿರಲಿ ಅಥವಾ ಸೌರ ಫಲಕವಾಗಿರಲಿ, ತನ್ನದೇ ಆದ ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಬಲವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಸಾಮಾನ್ಯವಾಗಿ ಈ EMF ಔಟ್ಪುಟ್ ವೋಲ್ಟೇಜ್ (U) ಗೆ ಹತ್ತಿರದಲ್ಲಿದೆ, ಆದರೆ ಯಾವಾಗಲೂ ಅದಕ್ಕಿಂತ ಸ್ವಲ್ಪ ಕಡಿಮೆ. ಇದು ಮೂಲದ ಆಂತರಿಕ ಪ್ರತಿರೋಧದಿಂದ ಉಂಟಾಗುತ್ತದೆ, ವೋಲ್ಟೇಜ್ನ ಭಾಗವು ಅನಿವಾರ್ಯವಾಗಿ ಇಳಿಯುತ್ತದೆ.

ಈ ಕಾರಣಕ್ಕಾಗಿ, ಇಎಮ್‌ಎಫ್‌ನ ಆದರ್ಶ ಮೂಲವು ಅಮೂರ್ತ ಪರಿಕಲ್ಪನೆ ಅಥವಾ ಭೌತಿಕ ಮಾದರಿಯಾಗಿದ್ದು ಅದು ನೈಜ ಜಗತ್ತಿನಲ್ಲಿ ಯಾವುದೇ ಸ್ಥಾನವಿಲ್ಲ, ಏಕೆಂದರೆ ಬ್ಯಾಟರಿ ರಿನ್‌ನ ಆಂತರಿಕ ಪ್ರತಿರೋಧವು ತುಂಬಾ ಕಡಿಮೆಯಿದ್ದರೂ ಸಹ ಸಂಪೂರ್ಣ ಶೂನ್ಯಕ್ಕಿಂತ ಭಿನ್ನವಾಗಿದೆ.

ಇಎಮ್ಎಫ್ನ ಆದರ್ಶ ಮತ್ತು ನಿಜವಾದ ಮೂಲ

ಭೇದಾತ್ಮಕ ರೂಪದಲ್ಲಿ

ಸೂತ್ರವನ್ನು ಆಗಾಗ್ಗೆ ಭೇದಾತ್ಮಕ ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸಲಾಗುತ್ತದೆ, ಏಕೆಂದರೆ ಕಂಡಕ್ಟರ್ ಸಾಮಾನ್ಯವಾಗಿ ಅಸಮಂಜಸವಾಗಿದೆ ಮತ್ತು ಅದನ್ನು ಸಾಧ್ಯವಾದಷ್ಟು ಚಿಕ್ಕ ವಿಭಾಗಗಳಾಗಿ ವಿಭಜಿಸುವುದು ಅಗತ್ಯವಾಗಿರುತ್ತದೆ. ಅದರ ಮೂಲಕ ಹಾದುಹೋಗುವ ಪ್ರವಾಹವು ಪರಿಮಾಣ ಮತ್ತು ದಿಕ್ಕಿನೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದೆ, ಆದ್ದರಿಂದ ಇದನ್ನು ಸ್ಕೇಲಾರ್ ಪ್ರಮಾಣವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ. ತಂತಿಯ ಮೂಲಕ ಫಲಿತಾಂಶದ ಪ್ರವಾಹವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕಾದರೆ, ಎಲ್ಲಾ ಪ್ರತ್ಯೇಕ ಪ್ರವಾಹಗಳ ಬೀಜಗಣಿತ ಮೊತ್ತವನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಈ ನಿಯಮವು ಸ್ಕೇಲಾರ್ ಪ್ರಮಾಣಗಳಿಗೆ ಮಾತ್ರ ಅನ್ವಯಿಸುವುದರಿಂದ, ಪ್ರಸ್ತುತವನ್ನು ಸ್ಕೇಲಾರ್ ಪ್ರಮಾಣವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಪ್ರಸ್ತುತ dI = jdS ವಿಭಾಗದ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ ಎಂದು ತಿಳಿದಿದೆ. ಅದರ ಮೇಲಿನ ವೋಲ್ಟೇಜ್ Edl ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ನಂತರ ಸ್ಥಿರ ಅಡ್ಡ ವಿಭಾಗ ಮತ್ತು ಸಮಾನ ಉದ್ದವನ್ನು ಹೊಂದಿರುವ ತಂತಿಗೆ, ಅನುಪಾತವು ನಿಜವಾಗಿರುತ್ತದೆ:

ಭೇದಾತ್ಮಕ ರೂಪ

ಆದ್ದರಿಂದ, ವೆಕ್ಟರ್ ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತದ ಅಭಿವ್ಯಕ್ತಿ ಹೀಗಿರುತ್ತದೆ: j = E.

ಪ್ರಮುಖ! ಲೋಹೀಯ ವಾಹಕಗಳ ಸಂದರ್ಭದಲ್ಲಿ, ಹೆಚ್ಚುತ್ತಿರುವ ತಾಪಮಾನದೊಂದಿಗೆ ವಾಹಕತೆ ಕಡಿಮೆಯಾಗುತ್ತದೆ, ಆದರೆ ಅರೆವಾಹಕಗಳಿಗೆ ಅದು ಹೆಚ್ಚಾಗುತ್ತದೆ. ಒಮೊವ್ ಕಾನೂನು ಕಟ್ಟುನಿಟ್ಟಾದ ಅನುಪಾತವನ್ನು ಪ್ರದರ್ಶಿಸುವುದಿಲ್ಲ

ಲೋಹಗಳು ಮತ್ತು ಮಿಶ್ರಲೋಹಗಳ ದೊಡ್ಡ ಗುಂಪಿನ ಪ್ರತಿರೋಧವು ಸಂಪೂರ್ಣ ಶೂನ್ಯಕ್ಕೆ ಹತ್ತಿರವಿರುವ ತಾಪಮಾನದಲ್ಲಿ ಕಣ್ಮರೆಯಾಗುತ್ತದೆ ಮತ್ತು ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸೂಪರ್ ಕಂಡಕ್ಟಿವಿಟಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.